1. Середня арифметична. 1
2. Середня гармонійна. 6
3. Середня геометрична. 8
4. Середня квадратична. 11
5. Мода і медіана. 18
Середня арифметична є найбільш поширеною-ненной серед середніх величин. Її застосовують в тих випадках, коли дані окремі об'єкти з індивідуальними значення-ми ознак, вираженими абсолютними показниками. Середню арифметичну визначають як відношення сум-ми індивідуальних значень ознак до їх кількості.
Розрізняють середню арифметичну просту і зважений-ву. Середню арифметичну просту застосовують в слу-чаї, якщо індивідуальні значення ознаки в сукупності зустрічаються по одному разу, а зважену - якщо індивідуальні значення ознаки представлені кількома об'єк-єктами.
Середню арифметичну просту визначають за фор-мулі:
n-число варіант.
Формула середньої арифметичної зваженої має вигляд:
де f-частота варіант.
Розглянемо методику розрахунку середньої арифметичної.
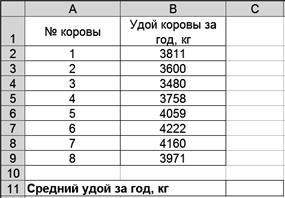
Приклад 1. Є дані по 8 коровам про їх удое за рік (табл. 2.1).
Т а б л і ц а 2.1
Потрібно визначити середній удій на одну корову за рік.
Так як дані індивідуальні значення удою молока по кожній корові, то середній удій визначається за формулою середньої арифметичної простої:
Таким чином, середньорічний удій від корови за рік становить 3883 кг.
Технологія виконання завдання втаблічном процесорі Microsoft Excel наступна.
1. Введіть вихідні дані відповідно до рис. 2.1.
2. Розрахуйте середній удій на корову за рік як середню арифметичну просту.
2.1. Виділіть клітинку С11.
2.2. Клацніть лівою кнопкою миші на панелі інструментів на кнопці <Вставка функции> або виконайте командуВставка, fx Функція. клацнувши по черзі лівою кнопкою миші.
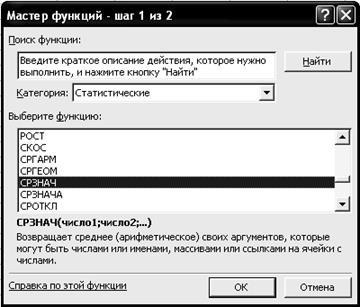
2.4. Клацніть лівою кнопкою миші на кнопці <ОК>.
2.5. На вкладці СРЗНАЧ встановіть параметри відповідно до рис. 2.3.
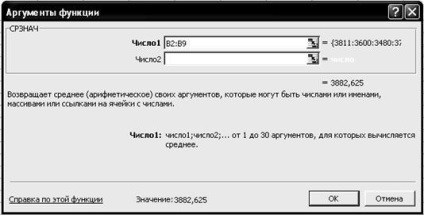
2.6. Клацніть лівою кнопкою миші на кнопці <ОК>.
Результати рішення виводяться на екран дисплея в наступному вигляді (рис. 2.4).
Приклад 2. Є дані по сільськогосподарському підприємству про поголів'я корів на фермах і середньорічному удое корови по кожній фермі (табл. 2.2).
Т а б л і ц а 2.2
Поголів'я корів і удій молока
Потрібно визначити середньорічний удій коро-ви за рік по господарству.
Оскільки індивідуальні значення ознаки в сукупність-ності зустрічаються кілька разів (наприклад, на фермі 1 - 230 разів), середня визначається за формулою середньої арифметичної зваженої. Для цього загальний валовий надій молока по сільськогосподарському перед- прийняттю необхідно розділити на все поголів'я корів:
Середньорічний удій молока корови в цілому по сільськогосподарському підприємству становить 4058 кг.
Технологія виконання завдання втаблічном процесорі Microsoft Excel наступна.
1. Введіть вихідні дані відповідно до рис. 2.5.
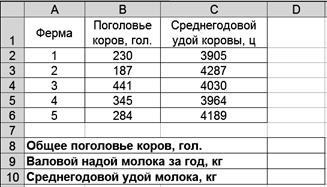
2. Розрахуйте загальне поголів'я.
2.1. Виділіть клітинку D8.
2.2. Клацніть лівою кнопкою миші на панелі інструментів на букві S кнопки <Автосумма> .
2.3. Виділіть комірки В2: В6.
2.4. натисніть
3. Розрахуйте валовий надій молока за рік.
3.1. Виділіть клітинку D9.
3.2. Клацніть лівою кнопкою миші на панелі інструментів на кнопці <Вставка функции> або виконайте командуВставка, fx Функція. клацнувши по черзі лівою кнопкою миші.
3.4. Клацніть лівою кнопкою миші на кнопці <ОК>.
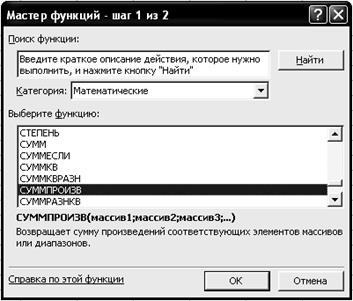
3.5. На вкладці СУММПРОИЗВ встановіть параметри відповідно до рис. 2.7.
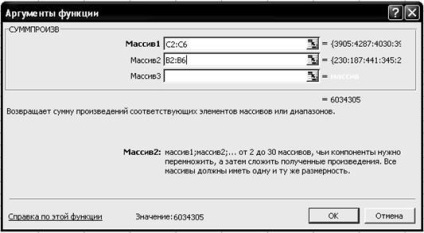
3.6. Клацніть лівою кнопкою миші на кнопці <ОК>.
4. Розрахуйте середньорічний удій молока від корови по сільськогосподарському підприємству як середню арифметичну взвешенную.Для цього введіть у комірку D10 формулу = D9 / D8.
Результати рішення виводяться на екран дисплея в наступному вигляді (рис. 2.8).
Середня гармонійна є зворотною величиною середньої арифметичної, розрахованої з зворотних зна-ний ознаки. Як частот в цьому випадку використовують-ся не одиниці сукупності, а твори цих одиниць на значення ознаки.
Середню гармонійну застосовують в тих випадках, коли відомі індивідуальні значення і обсяги ознаки, а частоти невідомі.
Формула середньої гармонійної має вигляд:
w - обсяги явища.
Розглянемо методику розрахунку середньої гармонійної.
Приклад. Є дані по сільськогосподарських підприємствах про загальні витрати на виробництво молока і собівартості 1 ц (табл. 2.3).
Т а б л і ц а 2.3