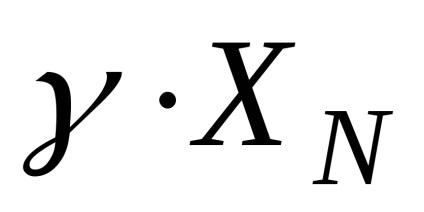3.5.1. Одноразове вимір з точним оцінюванням похибки
Переважна більшість вимірів - одноразові. Результати вимірювань включають в себе інструментальну, методичну та особисту складові, кожна з яких може бути систематичною і випадковою.
Систематичні похибки той чи інший спосіб намагаються виключити, залишаються НСП і випадкові похибки.
Межі НСП обчислюють за раніше наведеною формулою (3.8).
Якщо з попередніх багаторазових вимірювань відомі довірчі кордону випадкової похибки ε, то її підсумовують з НСП, причому НСП вважають як випадкову похибку. Сумарна гранична випадкова похибка Δ визначається за формулою:
Якщо значення ε невідомо, то вважають, що ε = 0.
Результат одноразового вимірювання R, при измеренном значенні Х, представляють у вигляді:
3.5.2. Одноразове вимір з наближеним оцінюванням похибки
Наближено похибка вимірювання оцінюють «зверху», знаючи межа допустимої похибки засобу вимірювання Δпр з паспорта. Часто в якості граничної похибки результату вимірювання приймають величину Δпр = ± (половина ціни поділки приладу), а іноді і Δпр = ± (ціна поділки приладу).
Похибка непрямих вимірювань
Визначення непрямих вимірювань наведено в підрозділі 2.1. Розрахунки похибок непрямих вимірювань можна звести до простих правил [4], позначивши: R-результат опосередкованих вимірювань; А, В, С-результат прямих вимірювань параметрів, на підставі яких розраховується R; Δ - абсолютна похибка вимірювання будь-якої величини, наприклад, ΔR, ΔА і т. Д .; δ - відносна похибка величини, наприклад: δR = ΔR / R; δА = ΔА / А і т. д.
Якщо R = А + В або R = А - В. то
т. е. абсолютна похибка результату непрямого вимірювання дорівнює сумі абсолютних похибок результатів прямих вимірювань.
Якщо R = А · В або R = А / В. то підсумовуються відносні похибкою ності:
Якщо R = кА. де до - коефіцієнт, то
де | k | - абсолютне значення коефіцієнта.
Приклад. Потужність Р. виділяється на резисторі з опором R при струмі I. дорівнює I2 · R. Тоді відносна похибка δP = 2 · δI + δR. Абсолютна похибка результату? Р = δP / Р. Результат буде представлений у вигляді: Р ±? Р.
Похибки шкальних приладів
При вимірах широко застосовуються шкальні (аналогові) прилади [9]. Вид шкали одного з приладів наведено на рис. 3.4. У нижній частині шкали цифра 2 означає клас приладу, тут же поміщають та інші спеціальні символи.
Р
Абсолютна похибка засобу вимірювання Δ визначається як різниця показань засоби вимірювання Х і показань еталонного приладу Хет:
Мал. 3.4. Вид шкали приладу
Абсолютна похибка є розмірної величиною. Поправка на неї дорівнює абсолютної похибки з протилежним знаком.
Відносна похибка визначається за рівнянням:
Відносна похибка є безрозмірною величиною і може виражатися десятковим дробом або у відсотках.
Наведена відносна похибка визначається як відношення абсолютної похибки приладу до нормованого значення шкали (до верхньої межі вимірювання) ХN:
Наведена відносна похибка у відсотках визначає клас точності приладу.
Приклад. Для зображеного на рис. 3.4 приладу класу точності 2 приведена похибка γ склала 2% = (0,02). Тоді абсолютна похибка показань Δ =