Полярна система координат визначається завданням деякої точки O. званої полюсом, що виходить з цієї точки променя OA (позначається також і як Ox), званого полярною віссю, і масштабу для зміни довжин. Крім того, при завданні полярної системи координат має бути визначено, які повороти навколо точки O вважаються позитивними (на кресленнях зазвичай позитивними вважаються повороти проти годинникової стрілки).
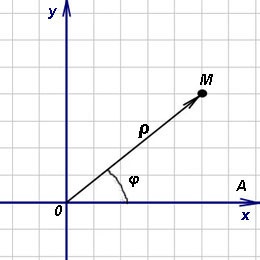
Отже, виберемо на площині (рисунок вище) деяку точку O (полюс) і деякий виходить з неї промінь Ox. Крім того, зазначимо одиницю масштабу. Полярними координатами точки M називаються два числа ρ і φ, перше з яких (полярний радіус ρ) дорівнює відстані точки M від полюса O. а друге (полярний кут φ, який називають також амплітудою) - кут, на який потрібно повернути проти годинникової стрілки промінь Ox до суміщення з променем OM.
Точку M з полярними координатами ρ і φ позначають символом M (ρ, φ).
Встановимо зв'язок між полярними координатами точки і її декартовими координатами. Будемо припускати, що початок декартової прямокутної системи координат знаходиться в полюсі, а позитивна піввісь абсцис збігається з полярною віссю. Нехай точка M має декартові координати x і y і полярні координати ρ і φ.Тогда
Полярні координати ρ і φ точки M визначаються по її декартових координатах наступним чином:
Для того, щоб знайти величину кута φ, потрібно, використовуючи знаки x і y. визначити квадрант, в якому знаходиться точка M. і, крім того, скористатися тим, що тангенс кута φ дорівнює.
Наведені вище формули називаються формулами переходу від декартових координат до полярних.
Приклад 1. В полярній системі координат на площині дано точки
Знайти полярні координати точок, симетричних цим точкам щодо полярної осі.
Рішення. При симетрії довжина променя не змінюється. Отже, перша координата - довжина променя - у симетричною відносно полярної осі точки буде як і у цієї точки. Як видно з малюнка на початку уроку, при побудові симетричною відносно полярної осі точки дану точку потрібно повернути навколо полярної осі на той же кут φ. Отже, в полярній системі координат другої координатою симетричною точки буде кут для вихідної точки, взятий з протилежним знаком, тобто -φ. Отже, полярні координати точки, симетричної даній щодо полярної осі будуть відрізнятися лише другий координатою, і ця координата буде з протилежним знаком. Полярні координати шуканих симетричних точок будуть наступними:
Приклад 2. У полярній системі координат на площині дано точки
Знайти полярні координати точок, симетричних цим точкам щодо полюса.
Рішення. При симетрії довжина променя не змінюється. Отже, перша координата - довжина променя - у симетричною відносно полюса точки буде як і у цієї точки. Симетрична щодо полюса точка виходить обертанням вихідної точки на 180 градусів проти годинникової стрілки, тобто на кут π. Отже, друга координата точки, симетричною даної щодо полюса розраховується як φ + π (якщо в результаті вийде чисельник більше знаменника, то віднімемо з отриманого числа один повний оборот, тобто 2π). Отримуємо наступні координати точок, симетричних даними щодо полюса:
Приклад 3. Полюс полярної системи координат збігається з початком декартових прямокутних координат, а полярна вісь збігається з позитивною полуосью абсцис. В полярній системі координат дано точки
Знайти декартові координати цих точок.
Рішення. Використовуємо формули переходу від полярних координат до декартових:
Отримуємо наступні декартові координати даних точок:
Приклад 4. Полюс полярної системи координат збігається з початком декартових прямокутних координат, а полярна вісь збігається з позитивною полуосью абсцис. У декартовій прямокутній системі координат дано точки
Знайти полярні координати цих точок.
Рішення. Визначаємо першу з полярних координат по формулі, а тангенс кута φ - другий з полярних координат як. Отримуємо наступні полярні координати даних точок: