Полярні і неполярні осі симетрії
а) полярні -на кінцях осі різні ел-ти фігури;
б) неполярні (біполярні) на кінцях осі однакові ел-ти фігури.
Поодинокі напрямки в кріталлах.
Єдине, що не повторюється в кристалі напрямок називає-ся одиничним.
У кубі немає одиничних напрямків, тут для любогонаправленія можна знайти симетрично-рівне.
6В навчальної символіці символіці Браве - осі симетрії позначаються як Ln
де підрядковий цифровий індекс п вказує на порядок
осі1 Графічно осі симетрії позначаються багатокутниками:
L6- L4 L3 L2
• площину симетрії Р
• Відображення в точці (інверсія) -
• центр симетрії, інверсії З
• Поворот з відображенням в точці - інверсійна вісь Lni - з рискою нагорі. Порядок осі - 1, 2, 3, 4, 6.
Інверсійні осі Дзеркальні осі
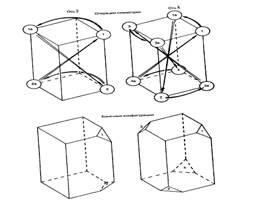
площину симетрії Р-максимум - 9
n центр симетрії С - кожній грані є назад паралельна
n L2 - може бути в фігурі - 1, 3, 4, 6; 2 (з інв. L4) - вісь нижчого порядку.
n L3 - може бути 1 або 4.
n L4 - може бути 1 або 3 (в т.ч. інверсійні).
n L6 - може бути одна.
n осі вищого порядку.
n Порядок осі = симетрії грані або кількості граней в вершині
Формула симетрії складається з записаних елементів симетрії даного кристала в певній послідовності: осі вищого порядку ® осі L2 ® площині симетрії ® центр симетрії. У кубічноїсингонії на другому місці завжди стоїть 4L3. Якщо який-небудь елемент відсутній, він опускається.
Кристалографічні координатні системи, їх параметри.
Щоб пов'язати координатні системи з симетрією кристала, коордінатниеосі поєднують з його особливими напрямами (осі симетрії і нормалі до площини симетрії)
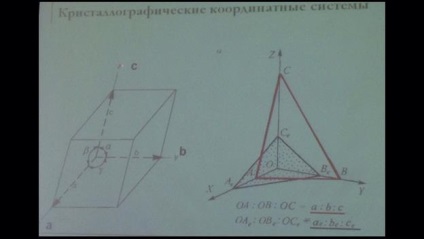
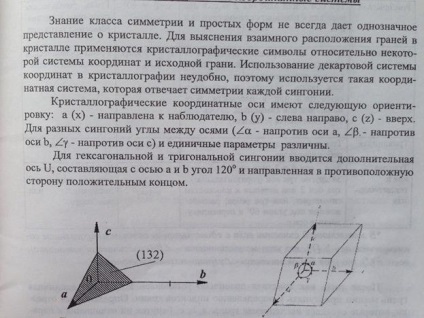
Правила установки кристалів різних сингоний.
16. Закон цілих чисел (Гаюї)
Другий закон клісталлографіі.
Ставлення відрізків, що відсікаються двома гранями кристала на координатних осях (або на трьох пересічних ребрах) ставляться один до одного як ціле, взаємно прості і малі числа. Для порівняння між собою параметрів граней кристала одна з його граней приймається за масштабну. Її називають одиничною гранню. При вимірі положення інших граней досліджуваного кристала параметри це межі приймають за одиницю.


Теорія дуже ретельним упаковок.
Теорія дуже ретельним упаковок куль обгрунтована академіком Миколою Васильовичем Бєловим. Атоми і іони кожного елемента характеризуються певним розміром - сферою дії, всередину меж, якої не можуть проникати інші частинки. В теорії кульових упаковок атоми, аніони і катіони представляються у вигляді нестискуваних куль відповідних радіусів і повинні бути упаковані в кристалі максимально щільно.
Теорія справедлива для іонних, молекулярних і металевих кристалів, в яких хімічний зв'язок ненаправленная і ненасичена.
АбАб гексагональнаяплотнейшаяупоковка - ГПУ 2х шарова
АБСАБС кубічна п у - КПУ - 3х шарова
У моноклінних лише одна з осей оптичної індикатриси збігається з єдиним особливим направленііем кристала, а дві інші фіксується щодо обраної координатної системи, тобто щодо ребер крісталла.В кристалах триклинной сингонії-кристали без особливих напрямків-все три осі індікатрісси можуть бути по-різному орієнтовані в кристалі.
Оптична індікатріса кубічних кристалів має форму кулі.
Гвинтові дислокація - забезпечує незникаючу сходинку для спірального зростання за рахунок зсуву однієї частини кристалів відносно іншої. Кристал з гвинтовою дислокацією вже не перебуває з паралельних атомних площин. скоріше його можна розглядати що складається з однієї атомної площини. закрученої у вигляді гвинтових сходів
Плоскі (двовимірні) дефекти -
1) Дефект упаковки - порушення послідовності шарів дуже ретельним упаковки куль
Для кубічної дуже ретельним упаковки АВСАВСАВС ... звичайний дефект шаровості
АВСАВААВС ... де АВА - дефект упаковки
Н ітевідние кристали (вискер). діаметр 1-10мкм. відношення довжини до діаметру більш 1000. вискер мають досконале будова. що наближає міцність віскерів до теоретичного для даної речовини порогу
полярні і неполярні осі симетрії
а) полярні -на кінцях осі різні ел-ти фігури;
б) неполярні (біполярні) на кінцях осі однакові ел-ти фігури.