Функція - одне з основних загальнонаукових понять; воно висловлює взаємозв'язок між різними об'єктами. Поняття функції склалося не відразу, перші спроби окреслити контури цього поняття були зроблені в кінці XVII ст. Родоначальником введення цього поняття з'явилися Лейбніц, а також брати Бернуллі. Сам термін «функція» належить Лейбніца і походить від лат. function «виконання, здійснення».
На початку XIX століття стало викристалізовуватися поняття функції як відповідності, правила, за яким незалежна змінна х з якогось безлічі X перетворюється в змінну у з іншого безлічі У «будь-яким чином».
Нехай дано деякий безліч значень величини х. т. е. деякий безліч точок на числовій осі Ох, позначимо його через D. Нехай також задані два безлічі (X, Y) R. Якщо для будь-якого значення х з множини X ставиться у відповідність за певним законом одне строго певне значення (взаємно однозначне відповідність) іншої величини у з безлічі у, то кажуть:
· Величина у є функція величини х або що величини х і у пов'язані між собою функціональною залежністю
· Задана функція, що відображає безліч Х в безліч У
· Задана функція y = f (x) на безлічі Х.
Дане визначення функції можна проілюструвати графічно:
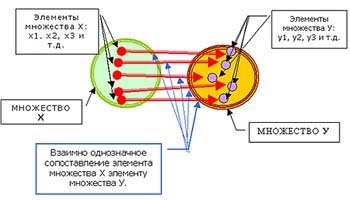
Значення аргументу х з області Х визначення функції у можна вибирати на свій розсуд довільно; тому величина х називається незалежною змінною. Значення ж функції у. коли значення незалежної змінної х вже призначено, довільно вибрати не можна. Це значення буде строго певним, саме тим, яке відповідає обраному значенням незалежної змінної. Значення функції залежать від значень, прийнятих незалежної змінної, і змінюються при її зміні. Тому функцію називають ще залежною змінною.
Як приклади розглянемо наступні функції.
Приклад 1. Температура T повітря в даному місці, яка вимірюється через кожну годину протягом доби, є функцією целочисленного аргументу-часу t, що приймає значення t = 0, 1, 2, 3. 23. Дійсно, кожному з цих значень величини t відповідає цілком певне значення величини T, і, значить, вона, в згоді з цим визначенням, є функцією величини t. Тут область визначення функції складається з 24-х "цілих" точок. Якщо вимірювання проводити не через кожну годину, а через кожну хвилину, то температура буде функцією целочисленного аргументу, що приймає вже 24 * 60 = 1440 послідовних цілих значень.
Приклад 2. Кожен студент вузу навчається в певній групі певного факультету. Якщо позначити через Х безліч студентів даного вузу, а через У - безліч навчальних груп, то можна сказати, що кожному елементу множини Х (кожному студенту) зіставлений єдиний елемент безлічі У (тобто та група, де він вчиться).