Кути розрізняють по їх величині. Великим вважається не той кут, сторони якого довший, а той, сторони якого сильніше розходяться нарізно. На рис. 13 уг. EDF більше, ніж кут 2, тому, що у першого боку сильніше розходяться нарізно. Зустрічаються кути, сторони яких розходяться нарізно абсолютно однаково; такі кути можна накласти один на інший так, що їх вершини співпадуть, а сторони зіллються. Кути, які можна таким чином накласти один на одного, вважаються рівними, хоча б сторони їх були неоднакової довжини.
На рис. 13 рівні, наприклад, уг. DEH і уг. DFH, уг. 2 і уг. а; ви можете переконатися в цьому, есля обведе один кут на прозорому папері і покриєте їм інший.
Якщо при накладенні порівнюваних кутів їх вершини і одна сторона збіглися, друга ж сторона накладається кута виявилася всередині або поза іншого кута, то такі кути, звичайно, не рівні. Той кут, який опинився всередині іншого, вважається меншим.
Розгляньте на тому ж рис. 13 кути, вершини яких лежать в точці D. Тут три кути: уг. EDF. уг. EDH і уг. HDF. Ви бачите, що обидва менших кута якраз заповнюють собою уг. EDF. який складається з них, як ціле зі своїх частин. Коли кути так розташовані, то кажуть, що уг. EDF є з у м м а кутів EDH і HDF. З л про ж тощо ь два кута значить знайти їх суму, т. Е. Той кут, який складеться, якщо прикласти їх один до одного, як показано на кресленні 13.
Якщо на рис. 13 від кута EDF відняти кут EDH. то залишиться уг. HDF; цей. кут називається р о з н о с т ь ю кутів EDF і EDH. Відняти один кут з іншого означає знайти їх різницю.
Які кути називаються рівними? - Чи залежить величина кута від довжини сторін? - Покажіть на кресленні, що називається сумою і різницею двох кутів.
Уявіть собі, що ми розводимо нарізно боку якого-небудь кута, - напр. уг. 1 (рис. 14). Від цього кут стане збільшуватися: він перетвориться спочатку в уг. 2, потім в уг. 3 і, нарешті, в уг. 4, сторони якого складають одну пряму лінію. Такі кути, як уг. 4, називаються р о з в е р н у т и м і кутами.
Чи може один розгорнутий кут бути більше або менше іншого розгорнутого? Звичайно, немає: адже всякі прямі лінії, якщо їх накласти одну на іншу, зливаються між собою; значить, повинні злитися при накладенні і всякі розгорнуті кути. Отже:
В с е р о з в е р н у т и е у г л и р а в н и м е ж д у с о б о ю.
Суміжні кути. Прямий кут
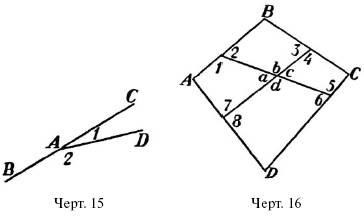
На рис. 15 ви бачите кути 1 і 2, які розташовані так, що вершини їх збігаються (в точці А) і одна сторона (AD) у них загальна, т. Е. Належить одночасно обом кутах, інші ж боку АВ і АС цієї пари кутів становлять одну пряму лінію. Кути, які так розташовані, називаються з м е ж н и м і. На рис. 16 ви бачите кілька пар суміжних кутів: уг. 1 і уг. 2; уг. 3 і уг. 4; уг. 5 і у м 6; у м а й у р b; уг. з і у м d. та ін.
Якщо кути, складові одну пару суміжних кутів, рівні між собою, - як уг. 7 і 8 на рис. 16, - то кожен з них називається прямим кутом. значить:
П р я м о й у г о л е с т ь о д и н і з д в у х р а в н и х з м е ж н и х у г л о в.
Так як обидва рівних суміжних кута складають разом один розгорнутий кут, то прямий кут є половина розгорнутого кута. Але все розгорнуті кути дорівнюють один одному; тому рівні і їх половини, т. е. прямі кути. значить:
В с е п р я м и е у г л и р а в н и д р у г д р у г у.
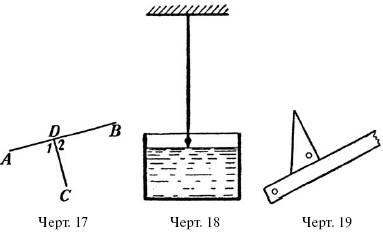
Прямі лінії, що зустрічаються під прямим кутом (рис. 17), називаються перпендикулярними один до одного. На рис. 17, наприклад, уг. 1 = уг. 2, а так як ці кути суміжні і притому рівні, то вони - прямі. Тому CD перпендикулярно до АВ і АВ перпендикулярно до CD.
Слово «перпендикулярний» не треба змішувати зі словом «вертикальний». В е р т і до а л ь н о м, або про т в е з н о м, називають будь-яку пряму лінію, що має напрямок вільно звішується навантаженої нитки.
Всі ті лінії, які складають з вертикальною лінією прямий кут, називаються г о р и з о н т а л ь н им і. Горизонтальні, наприклад, всі лінії, проведені по поверхні води (рис. 18). Стрімке напрямок перевіряють схилом (рис. 18); горизонтальне - плотничий рівнем.
На папері прямий кут креслять допомогою лінійки і креслярського трикутника (рис. 19). Перевірити, чи правильно виготовлений креслярський трикутник, можна так. Провівши по лінійці пряму лінію і накресливши за допомогою трикутника іншу пряму до неї, перпендикулярну, прикладають креслярський трикутник прямим кутом до суміжного кутку: якщо ці кути рівні, то трикутник виготовлений правильно.
Кути, менші, ніж прямий, називаються о с т р и м і; більші, ніж прямий, - т у п и м і.
Повторювальні питання до §§ 6 і 7
Який кут називається розгорнутим? - Які кути називаються суміжними (накресліть кілька таких кутів)? - Який кут називається прямим? - Як називається кут, який дорівнює суміжному з ним? - Чи можуть прямі кути мати різну величину? - Поясніть значення слів: перпендикулярний, вертикальний, стрімкий, горизонтальний. - Як креслити перпендикулярні прямі допомогою креслярського трикутника? - Які кути називаються гострими? Тупими? Накресліть кілька гострих і кілька тупих кутів.
1. Уміння креслити взаємно-перпендикулярні прямі дозволяє будувати так зв. «Графіки», т. Е. Ламані (або криві) лінії, які наочно показують хід зміни явищ. Нехай потрібно побудувати графік температури за тиждень за наступними даними:
Зобразимо ці температури поруч перпендикулярів до одній прямій, наведених на рівних відстанях один від одного: довжина перпендикулярних відрізків буде зображувати температуру дня. Верхівки перпендикулярів з'єднаємо прямими лініями: отримана ламана лінія і є «графік температур».
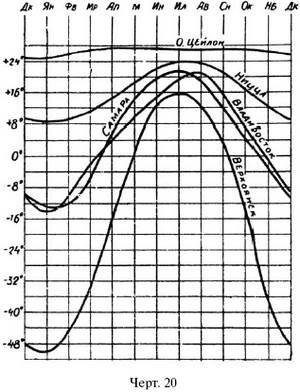
2. На рис. 20 зображені графіки річного ходу температури повітря в різних місцях земної кулі: на о-ві Цейлон, в Ніцці, в Самарі, у Владивостоці і в Верхоянську. Розглядаючи ці графіки, ми можемо відповісти собі на ряд можуть виникнути питань, наприклад:
a) Яка температура в середньому за багато років у всіх на званих місцях 1 мая?
Про т в е т. На Цейлоні + 27 ° в Ніцці + 18 °, в Самарі + 15 °, у Владивостоці + 10 °, в Верхоянську 0 °.
b) Які дні в році (в середньому) найспекотніші і найхолодніші в Верхоянську?
Про т в е т. У Верхоянську, Владивостоці та Самарі.
d) Яка різниця між найвищою і найнижчою середньою температурою в Ніцці? В Самарі?
Про т в е т и. У Ніцці середня температура коливається від + 9 ° до + 24 °; в Самарі - від мінус 10 ° до + 21 °.
Властивість суміжних кутів
Сума обох суміжних кутів, очевидно, дорівнює розгорнутому куті. Але розгорнутий кут дорівнює двом прямим кутам, взятим разом. Тому:
З у м м а о б о і х з м е ж н и х у г л о в р а в н а д в у м п р я м и м у г л а м.
Наприклад, на рис. 21 уг. 1 + уг. 2 = двом прямим кутам.
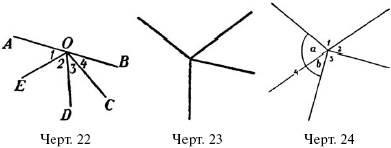
Буває, що по одну сторону прямої розташоване не два кута, як у випадку суміжних кутів, а кілька кутів, - як на рис. 22. Легко переконатися, що сума цих кутів також дорівнює двом прямим: з них завжди можна скласти одну пару суміжних кутів (на рис. 22 кути АОD і DOВ, або АОЄ і ЕОВ).
Подібним же чином можна знайти, чому дорівнює сума кутів. розташованих навколо спільної вершини, як на рис. 23. Продовживши одну зі сторін за загальну вершину (рис. 24), отримаємо дві групи кутів: групу 1 і а, сума яких дорівнює двом прямим (чому?), І групу кутів 2, 3, Ь, сума яких дорівнює також двом прямим кутах; значить, сума всіх кутів навколо спільної вершини дорівнює 4 прямим кутам.
Чому дорівнює сума суміжних кутів? - Сума декількох кутів, розташованих по одну сторону прямої лінії? - Сума всіх кутів, розташованих навколо спільної вершини?
1) На рис. 25 уг. 1 = 48 °. Знайти інші кути.
2) На рис. 25 уг. b = 136 °. Знайти інші кути.
Коли дві прямі лінії перетинають один одного (рис. 25), вони утворюють дві пари кутів, сторони яких складають продовження одні інших: одна пара - уг. 1 і уг. 2; інша - уг. а й уг. b. Особливість протилежних кутів та, що кути, складові таку пару, завжди рівні між собою: у м 1 = уг. 2, уг. а = у м b. Дійсно, якщо наприклад (рис. 25) уг. 1 = 40 °, то уг. b = 180 ° - 40 ° = 140 °, уг. 2 = 180 ° - 140 ° = 40 °, і уг. а = 180 ° - 40 ° = 140 °; ми бачимо, що уг. 1 = уг. 2, і уг. а = уг. b. Взагалі, так як уг. 1 разом з кутом а дорівнює двом прямим (чому?), А уг. 2 разом з тим же кутом а також дорівнює двом прямим, то ясно, що уг. 1 повинен дорівнювати уг. 2. Отже:
П р о т і в про п про л про ж зв и е у г л и р а в н и.
Які кути називаються протилежними? знаєте властивість протилежних кутів?
До сих пір ми говорили лише про прямі лініях. З до р і ш и х ліній зупинимося на о к р у ж н о с т і (рис. 26). Окружність креслять циркулем. Вістря ніжки розсунутого циркуля встромляють в папір, іншу ж ніжку з олівцем обертають навколо першої; коли олівець зробить повний оборот, він проведе на папері замкнуту криву - окружність. Та точка, в яку було встромлений вістря циркуля, називається ц е н т р о м окружності. Зрозуміло, що всі крапки окружності віддалені від центру на однакову відстань; це відстань називається р а д і у с о м окружності. значить:
Про до р у ж н о с т ь е с т ь к р і в а я л і н і я, в с е т о ч к и к о т о р о м о д и н а к о в о у д а л е н и о т о д н о м
т о ч к и, н а з и в а е м о й ц е н т р о м.
Пряма, що з'єднує дві точки кола через центр, називається д і а м е т р о м.
Будь-яка частина окружності називається її д у р о ю (рис. 27).
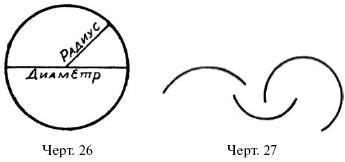
Плоска фігура, обмежена колом, називається до р у г о м.
Що таке коло? Центр? Радіус? Дуга? - Покажіть все це на кресленні. - Чи всі радіуси одному колі рівні між собою? - Що більше: діаметр або радіус? У скільки разів?
3. Гудок заводу чути на 4 км. Накреслити в масштабі 1 км в 1 см кордон місцевості, де чути гудок цього заводу.
Р і ш е н і е. Навколо точки, що позначає стан заводу, накреслити коло радіусом 4 см.
4. Радіус кола 100 см. Деяка точка віддалена від центру на 40 см. Лежить вона всередині кола або поза ним? Яке найближча відстань від цієї точки до кола?
Р і ш е н і е. Точка лежить всередині кола. Найближча відстань її від окружності треба вважати уздовж діаметра, проведеного через цю точку; воно дорівнює 60 см. Подальше відстань (уздовж того ж діаметру) - 140 см.