Перша симплекс-таблиця піддається перетворенню, суть якого полягає в переході до нового опорного рішення.
Алгоритм переходу до наступної таблиці такий:
- проглядається другий рядок (індексна) таблиці і серед коефіцієнтів цього рядка (виключаючи стовпець вільних членів) вибирається найбільший негативний число при знаходженні max. або найбільший позитивний при завданні на min. Якщо такого (при знаходженні max - негативного, а при знаходженні min - позитивного) немає, то вихідне базисне рішення є оптимальним і дана таблиця є останньою;
- проглядається стовпець таблиці. відповідає обраному негативному (позитивному) коефіцієнта у другому рядку - ключовий стовпець, і в цьому стовпці вибираються положітельниекоеффіціенти. Якщо таких немає, то цільова функція необмежена на області допустимих значень змінних і завдання рішень не має;
- серед обраних коефіцієнтів стовпця вибирається той, для якого абсолютна величина відносини відповідного вільного члена (що знаходиться в стовпці вільних членів) до цього елементу мінімальна. Цей коефіцієнт називається що дозволяє. а рядок, в якій він знаходиться, ключовий;
- в подальшому базисна змінна. відповідає рядку дозволяє елемента, повинна бути переведена в розряд вільних. а вільна змінна, що відповідає стовпцю дозволяє елемента, вводиться в число базисних. Будується нова таблиця, яка містить нові назви базисних змінних;
- дозволяє елемент замінюємо на:
- помножимо кожен елемент ключовий рядки (виключаючи дозволяє елемент) на і отримані значення запишемо в рядок зі зміненою базисної змінної нової симплекс таблиці;
- помножимо кожен елемент ключового стовпця (виключаючи дозволяє елемент) на і отримані значення запишемо в стовпчик зі зміненою вільної змінної нової симплекс таблиці;
- стовпець. у якого в ключовий рядку є 0. в новій таблиці будеттакім же;
- рядок. у якій в ключовому стовпці є 0. в новій таблиці буде такий же;
- в інші клітини нової таблиці записується результат перетворення елементів старої таблиці:
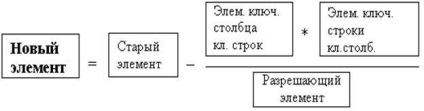
В результаті отримують нову симплекс-таблицю, що відповідає новому базисному рішенням. Інакше схему перетворення елементів симплекс-таблиці (крім провідного рядка і ведучого шпальти) називають схемою "прямокутника". Перетворений елемент і відповідні йому три сомножителя якраз і є вершинами "прямокутника".
В іншому випадку, переходимо до нової симплекс таблиці по вище описаним алгоритмом.
Розглянемо порядок вирішення завдання за допомогою симплекс-таблиць на прикладі.