Пошук екстремуму функції однієї змінної
Пошук екстремуму функції включає в себе завдання знаходження локального і глобального екстремуму. За допомогою вбудованих функцій вирішується тільки завдання пошуку локального екстремуму. Щоб знайти глобальний максимум (або мінімум), потрібно спочатку вирахувати всі їх локальні значення і потім вибрати найбільший (найменший), або попередньо просканувати з деяким кроком розглянуту область, щоб виділити з неї найбільших (найменших) значень функції і здійснити пошук глобального екстремуму, вже перебуваючи в його околиці.
Для пошуку локальних екстремумів є дві вбудовані функції, які можуть застосовуватися як в межах обчислювального блоку, так і автономно.
- Minimaze (f ', х1. Хм) - вектор значень аргументів, при яких функція досягає мінімуму;
- Maximaze (f ', х1. Хм) - вектор значень аргументів, при яких функція досягає максимуму;
Всім аргументів функції f попередньо слід привласнити деякі значення, причому для тих змінних, за якими проводиться мінімізація, вони будуть сприйматися як початкові наближення.
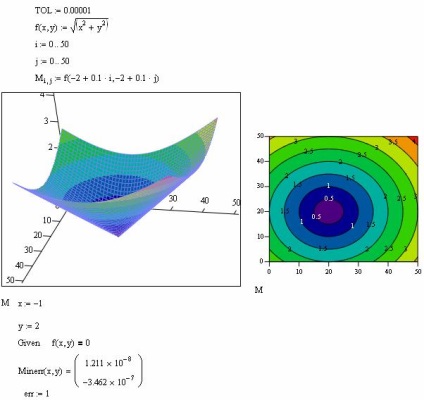
Пошук екстремуму функції кількох змінних.
Обчислення екстремуму функції багатьох змінних не несе принципових особливостей в порівнянні з функціями однієї змінної. Але також пошук екстремуму можна організувати за допомогою функції Minerr:
- x1: = C1. хм: = См - початкові значення для невідомих;
- Given - ключове слово;
- система алгебраїчних рівнянь і нерівностей, записана логічними операторами;
- Minerr (x1. Хм) - наближене рішення системи щодо змінних x1 ,. хм. мінімізує нев'язність системи рівнянь.