Резонансні явища в електричних ланцюгах
Застосування послідовного коливального контуру
Енергетичні співвідношення в послідовному коливальному контурі при резонансі
Вплив внутрішнього опору джерела сигналу на АЧХ контуру
Послідовний коливальний контур
Резонансні явища в електричних ланцюгах
Послідовний коливальний контур
Резонансом електричного кола називають явище звернення в нуль її реактивного опору. Частоту, на якій має місце цей факт, називають резонансною. Резонанс може виникати тільки в ланцюгах, що мають хоча б по одному реактивному елементу різного типу провідності.
Резонанси можуть мати місце як в окремих гілках електричного кола, так і в контурах. Тому в ланцюгах з декількома реактивними елементами різного типу може бути кілька резонансних частот.
У радіотехніці резонансні явища в електричних ланцюгах широко використовують для виділення смуги частот і посилення сигналів.
Ланцюг з послідовним з'єднанням елементів називають послідовним коливальним контуром. Так як реальні індуктивності і ємності мають втрати, то це враховано на схемі послідовно включеним в ланцюг малим еквівалентним опором втрат (рис. 15.1).
Опір цьому ланцюзі дорівнюватиме
де - модуль, і - активна і реактивна складові, - фаза повного опору.
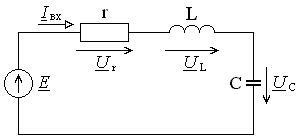
Мал. 15.1. Послідовний коливальний контур
На резонансній частоті реактивна складова повного опору звертається в нуль, тобто виконується умова
Звідси отримуємо формулу для розрахунку резонансної частоти через параметри послідовного коливального контуру
На частотах менше резонансної реактивний опір ланцюга негативно, тобто носить ємнісний характер, так як опір ємності більше опору індуктивності і є переважаючим. На частотах більше резонансної реактивний опір послідовного коливального контуру позитивно і має індуктивний характер, так як в цьому випадку опір індуктивності стає більше опору ємності.
Перетворимо вираз (15.1) з урахуванням введеного поняття резонансної частоти:
Величину, що має розмірність опору, називають хвильовим або характеристичним опором контуру, причому
Ставлення характеристичного опору до опору втрат називають добротністю контуру і позначають символом, а зворотний йому величину - загасанням:
Контури низької якості мають добротність менше 50. Для контурів середньої якості виконується співвідношення, для контурів хорошої якості - і для контурів високої якості -.
Вираз в круглих дужках у формулі (15.4) позначають грецькою буквою і називають відносною розладу контура
За змістом, відносна розладі характеризує в відносних одиницях відхилення частоти джерела сигналу від резонансної частоти контуру.
З урахуванням введених позначень формулу опору (15.4) можна записати в більш компактній формі:
Струм в ланцюзі можна знайти за законом Ома:
де - початкова фаза джерела ЕРС, - фаза повного опору в іншій формі запису.
На резонансній частоті струм максимальний і дорівнює
Нормована амплітудно-частотна (АЧХ)
і фазочастотная характеристики (ФЧХ)
струму наведені на рис. 15.2.
На резонансній частоті відносна розладі (15.7) дорівнює нулю. Тому
Отже, на резонансній частоті амплітуди напруг на індуктивності і ємності рівні один одному і в раз більше амплітуди ЕРС:
Тому резонанс в послідовному коливальному контурі називають резонансом напруг. Векторна діаграма напруг для контуру на частоті резонансу приведена на рис. 15.3.
Область частот, на кордонах якої струм зменшується в раз щодо свого максимального значення, називають смугою пропускання. На межах смуги пропускання відповідно до формули (15.9) виконується умова
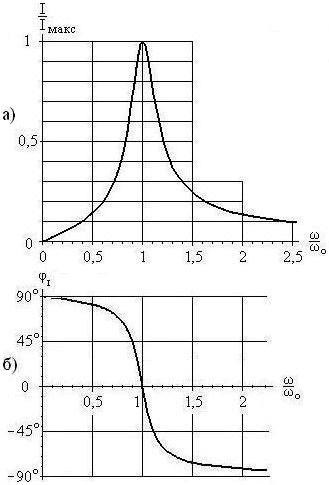
Мал. 15.2. Амплітудно-частотна (а) і фазочастотная (б) характеристики струму в послідовному коливальному контурі
Мал. 15.3. Векторна діаграма послідовного коливального контуру на резонансній частоті
Звідси отримуємо значення відносної розладу на межах смуги пропускання
Практично завжди можна вважати, що. Тому є малою величиною і без великої погрішності, використовуючи формулу (15.7), відносну расстройку на межах смуги пропускання можна замінити наближеним виразом:
де, а - смуга пропускання контуру. Об'єднуючи вирази (15.14) і (15.16), остаточно одержуємо досить точну формулу розрахунку смуги пропускання
Для порівняння контурів один з одним зручно використовувати амплітудно-частотні характеристики, побудовані в залежності від відносної розладу (рис. 15.4), а не від відносної частоти як на рис. 15.2.
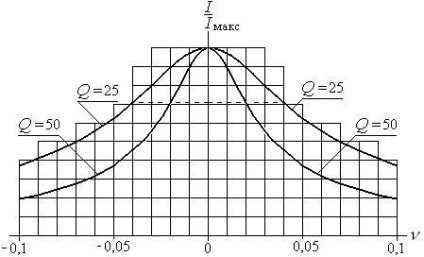
Мал. 15.4. Амплітудно-частотні характеристики послідовного коливального контуру в залежності від відносної розладу
Слід звернути увагу на те, що величина напруги на ємності
досягає максимуму на частоті менше резонансної, а величина напруги на індуктивності досягає максимуму на частоті більше резонансної.