Елементарна теорія ПОХИБОК
Абсолютна і відносна похибки. Знак рівності в наближених обчисленнях має інший сенс, як в алгебрі. Рівність означає не збіг значень, а лише близькість значень. Точність наближеного рівності, тобто ступінь близькості точного значення і наближеного. характеризує абсолютна похибка.
На практиці замість абсолютної похибки, яка зазвичай невідома, використовують граничну абсолютну похибку.
причому слово гранична для стислості опускають. Якщо цікавить точність вже проведеного розрахунку, то за беруть число, яке можливо ближче до "істинної" похибки. Називають це оцінкою похибки. Оцінка похибки може бути грубої або більш точною. Похибка може бути задана заздалегідь, тоді обчислення проводиться так, щоб це нерівність виконувалося.
Для того щоб записати, що є наближеним значенням з абсолютною похибкою. пишуть:
Відносною похибкою. часто виражається у відсотках, називають величину таку, що
Відносна похибка більш повно характеризує ступінь точності наближеного числа, оскільки можна порівнювати точність завдання величин, як істотно розрізняються по порядку, так і виражених в різних одиницях виміру.
Вірні і сумнівні цифри. Значущу цифру називають вірною у вузькому сенсі. якщо абсолютна похибка числа не перевищує 1/2 одиниці розряду, що відповідає цій цифрі.
маємо; також. Отже, вірні цифри в вузькому сенсі 9 і 3. значущої цифри називають вірною в широкому сенсі. якщо абсолютна похибка числа не перевищує одиниці розряду, що відповідає цій цифрі (В прикладі 9, 3 і 4). Цифри, які стоять в більш молодших розрядах, називають сумнівними.
Послідовність виконання роботи
Приклад 1. Задані точне і наближене значення числа. Знайти абсолютну і відносну похибки (рішення приведено на рис. 2.1)
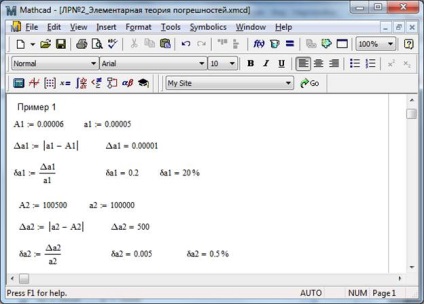
Мал. 2.1 - Рішення прикладу 1
Приклад 2. Знайти граничні абсолютні і відносні похибки чисел і. якщо вони мають тільки вірні цифри: а) у вузькому сенсі, б) в широкому сенсі.
Рішення завдання наведено на рис. 2.2
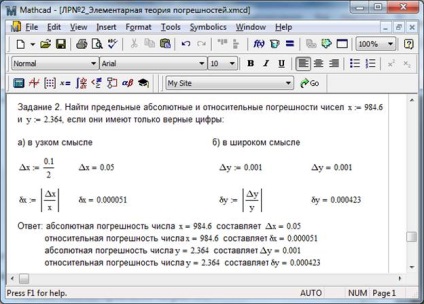
Мал. 2.2 - Рішення прикладу 2
Приклад 3. Задано число і відносна похибка. Визначити кількість вірних цифр числа по його відносної похибки.
Рішення: оскільки і. то число має, принаймні, дві цифри, вірних у вузькому сенсі. Визначимо абсолютну похибку:
Значить, у вузькому сенсі вірними є цифри 2 і 3.
Приклад 4. Нехай. . Визначити кількість вірних цифр в числі.
Рішення: оскільки і. то число має, принаймні, одну цифру, вірну у вузькому сенсі (цифра 9). Перевіримо цей результат, використовуючи визначення цифри, вірною у вузькому сенсі.
Для цього визначимо абсолютну похибку:
Отримана абсолютна похибка не перевищує половину одиниці розряду сотень. Отже, цифра 9 вірна у вузькому сенсі, як по відносної похибки, так і за абсолютною.
Приклад 5. Нехай. . Визначити всі вірні цифри числа.
Рішення: оскільки. то число має, принаймні, чотири цифри, вірних у вузькому сенсі (цифри 2, 4, 3, 0). обчислимо
Приклад 6. При зважуванні двох вантажів отримали наступні значення їх мас кг і кг. Вважаючи абсолютну похибку зважування дорівнює 1 г, визначити відносну похибка вимірювання мас тел. Яке з тіл зважено більш точно?
Рішення прикладу на рис. 2.3.
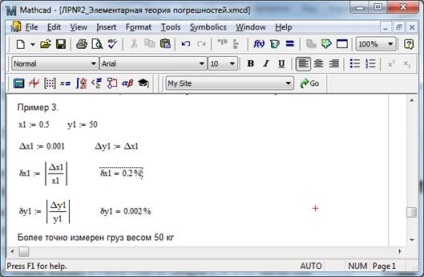
Мал. 2.3 - Рішення прикладу 6
Приклад 7. Визначити, яке рівність точніше або
Рішення: знайдемо значення даних виразів з бóльшим числом десяткових знаків:. . Обчислимо граничні абсолютні похибки, округляючи їх з надлишком:
Граничні відносні похибки становлять:
Так як . то рівність є більш точним.
Приклад 8. Округлити сумнівні цифри числа, залишивши вірні знаки:
а) у вузькому сенсі;
б) в широкому сенсі.
Визначити абсолютну похибку результату.
а) нехай. Згідно з умовою, похибка; це означає, що в числі вірними у вузькому сенсі є цифри 7, 2, 3. За правилами округлення знайдемо наближене значення числа, зберігши десяті частки:
Отримана похибка більше 0,05; значить, потрібно зменшити число цифр в наближеному числі до двох:
Тому обидві цифри, що залишилися вірні у вузькому сенсі.
б); тоді. В даному числі вірними в широкому сенсі є три цифри, тому округляем його, зберігаючи ці три цифри:
Значить, і в округлені числі всі три цифри вірні в широкому сенсі.
Приклад 9. Знайти граничні абсолютні і відносні похибки чисел, якщо вони мають тільки вірні цифри:
а) у вузькому сенсі;
б) в широкому сенсі
Рішення: а) так як всі чотири цифри вірні у вузькому сенсі, то абсолютна похибка. а відносна похибка
б) так як всі п'ять цифр числа вірні в широкому сенсі, то:;
Приклад 10. Обчислити і визначити похибки результату.
4. Контрольні питання:
1. Що таке абсолютна і відносна похибки?
2. Що означає цифра, вірна в широкому і вузькому сенсах?
3. Як визначити кількість вірних цифр по відносної похибки наближеного числа?
4. Як визначаються абсолютна і відносна похибки в арифметичних діях?
Варіанти завдань до лабораторної роботи 2
1) Визначити, яке рівність точніше.
2) Округлити сумнівні цифри числа, залишивши вірні знаки:
а) у вузькому сенсі; б) в широкому сенсі.
Визначити абсолютну похибку результату.
3) Знайти граничні абсолютні і відносні похибки
чисел, якщо вони мають тільки вірні цифри:
а) у вузькому сенсі; б) в широкому сенсі.
Варіанти завдань наведені в табл. 1.1.