Квиток № 1 Інформація - відомості про об'єкти і явища навколишнього середовища, їх параметри, властивості і стан, які сприймають інформаційні системи (живі організми, керуючі машини та ін.) В процесі життєдіяльності і роботи. Дані - 1) відомості, необхідні для будь-якого висновку, рішення, процедури (наприклад: багато даних, цифрові дані); 2) підстави для чогось, якості (наприклад: голосові дані, мати всі дані для отримання премії). Електронна обчислювальна машина (ЕОМ) - обчислювальна машина, побудована з використанням в якості функціональних елементів електронних пристроїв замість механічних. Термін вживався для відмінності від історичного предшественніка- механічної обчислювальної машини. Більшість сучасних процесорів для персональних комп'ютерів в загальному засновані на тій чи іншій версії циклічного процесу послідовної обробки даних, винайденого Джоном фон Нейманом. Дж. Фон Нейман придумав схему побудови комп'ютера в 1946 році. Відмінною особливістю архітектури фон Неймана є те, що інструкції і дані зберігаються в одній і тій же пам'яті. У різних архітектурах і для різних команд можуть знадобитися додаткові етапи. Наприклад, для арифметичних команд можуть знадобитися додаткові звернення до пам'яті, під час яких проводиться зчитування операндів і запис результатів. Квиток № 2 • Система счісленія- символічний метод запису чисел, подання чисел за допомогою письмових знаків. Число - це деяка абстрактна сутність для опису кількості. • Цифри - це знаки, які використовуються для запису чисел. Цифри бувають різні: найпоширенішими є арабські цифри, що подаються відомими нам знаками від нуля (0) до дев'яти (9); менш поширені римські цифри, ми їх можемо іноді зустріти на циферблаті годинника або в позначенні століття (XIX століття). Отже запам'ятаємо: • число - це абстрактна міра кількості; • цифра - це знак для запису числа. Оскільки чисел набагато більше ніж цифр, то для запису числа зазвичай використовується набір (комбінація) цифр. Тільки для невеликої кількості чисел - для найменших за величиною - буває достатньо однієї цифри. Існує багато способів запису чисел за допомогою цифр. Кожен такий спосіб називається системою числення. Величина числа може залежати від порядку цифр у записі, а може і не залежати. Це властивість визначається системою числення і служить підставою для найпростішої класифікації таких систем.
Системи числення. Поняття, характеристики, різновиди, приклади. [Ключові терміни: система числення, характеристики (підстава, алфавіт системи числення). Різновиди систем числення: непозиційної, позиційні (з постійним, змінним підставою). Приклади систем числення.]
Система числення - символічний метод запису чисел, подання чисел за допомогою письмових знаків.
Система числення - спосіб запису чисел за допомогою набору спеціальних знаків,
званих цифрами. Системи числення бувають позиційні і непозиційної.
У позиційних системах числення величина, що позначається цифрою у записі числа,
залежить від її положення в числі (позиції). Приклад позиційної системи числення - це
арабська (наша з вами), а непозиционной - римська.
Підстава системи числення - це кількість різних знаків або символів, які використовуються для зображення цифр в даній системі. Наприклад, у десятковій системі використовуються десять символів (цифри від 0 до 9), отже підставу системи десять.
Алфавіт системи числення - це сукупність символів, що використовуються в даній системі числення.
Кількість інформації, що міститься в символьному повідомленні, так само Кхi, де К - число символів в тексті повідомлення, аi- інформаційний вага символу, який знаходиться з рівняння 2 ^ i = N, гдеN- потужність використовуваного алфавіту
Всі системи числення підрозділяються на два класи - позиційні і непозиційної.
У непозиційних системах числення від положення цифри в запису числа не залежить величина, яку вона позначає.
1.1. Позиційні системи числення.
У позиційних системах числення величина, що позначається цифрою у записі числа, залежить від її позиції. Кількість різних цифр р, використовуваних в позиційній системі, визначає назву системи числення і називається підставою р-ой системи числення.
Позиційна система числення - система числення, в якій значення кожного числового знака (цифри) в запису числа залежить від його позиції (розряду).
Запис довільного числа x в P-ічной позиційній системі числення грунтується на поданні цього числа у вигляді многочлена
x = anPn + an-1Pn-1 +. + A1P1 + a0P0 + a-1P-1 +. + A-mP-m
Арифметичні дії над числами в будь-який позиційній системі числення виробляються за тими ж правилами, що і десятковій системі, так як всі вони грунтуються на правилах виконання дій над відповідними многочленами. При цьому потрібно тільки користуватися тими таблицями додавання і множення, які відповідають даній підставі P системи числення.
У непозиційних системах числення величина, яку позначає цифра, не залежить від положення в числі. При цьому система може накладати обмеження на положення цифр, наприклад, щоб вони були розташовані в порядку убування.
Прикладом непозиционной системи числення служить римська система, в якій замість цифр використовуються латинські літери.
Наприклад: Число 242 можна записати ССXLII (тобто 100 + 100 + (50-10) + 1 + 1).
розглянемо особливий різновид позиційних нумераций зі змінним підставою (раніше приводилися міркування ставилися до нумерації з фіксованими підставами - 2, 8, 10 та іншими).
З ними нам доводиться зустрічатися, але, в основному, ні до обчисленнях. Скажімо, міри довжини, заходи ваг, в яких використовуються не-десяткові коефіцієнти при переході від "молодших розрядів" вимірювання до "старшим" (наприклад, фути-ярди-милі).
Приклад же з вимірюванням часу, взагалі, універсальний: секунди-хвилини-години. Скажімо, зараз у мене 17:47:00. Ніщо не заважає замінити цю форму запису на більш компактну (174700), не забуваючи при тому, що діапазон значень молодшого (нульового) розряду 0..9, наступного лівіше (першого) - 0..5, далі, відповідно, - 0. .9, 0..5, а потім і зовсім "дивний" діапазон 0..24 (іноді замінюється на 0..12).
Системи числення. двоичная, десяткова, одинична, троичная, шістнадцяткова, восьмерична, і т.д.
Поняття ваг символу алфавіту системи числення, розряду числа. Відмінність виконання арифметичних операцій в різних системах числення. [Значення поняття ваги символу алфавіту системи числення, в числі, ваги розряду. Відмінність виконання арифметичних операцій в позиційних системах числення з різним підставою (модуль рахунку).]
інформаційний вага символу двійкового алфавіту прийнятий за одиницю інформації і називається 1 біт. Вводиться формула:, де- інформаційний вага кожного символу, а- потужність алфавіту, такжеI- кількість інформації. яке несе один знак.
Кількість інформації, що міститься в символьному повідомленні, так само К х i, де К - число символів в тексті повідомлення а i - інформаційний вага символу, який знаходиться з рівняння 2i = N, де N - потужність використовуваного алфавіту.
Під алфавітом ми будемо розуміти набір букв, розділових знаків, цифр, дужок та ін. Символів, використовуваних в тексті. В алфавіт також слід включити і пробіл, т. Е. Пропуск між словами.
Будемо позначати цю величину буквою N. Наприклад »потужність алфавіту з російських букв та зазначених додаткових символів дорівнює 54: 33 букви + 10 цифр + 11 знаків пунктуації, дужки, пробіл.
1 кілобайт = 1 Кб = 1024 байта
1 мегабайт = 1 Мб = 1024 кілобайт
1 гігабайт = 1 Гб = 1024 мегабайта
Якщо пронумерувати розряди цілого числа справа наліво, починаючи від 0
для розряду одиниць, то вага будь-якого розряду виходить зведенням підстави
системи числення в ступінь, значення якої дорівнює номеру розряду.
Системою числення називається сукупність прийомів найменування і записи чисел. У будь-якій системі числення для подання чисел вибираються деякі символи (їх називають цифрами), а інші числа виходять в результаті будь-яких операцій над цифрами даної системи числення.
Система називається позиційною. якщо значення кожної цифри (її вага) змінюється в залежності від її положення (позиції) в послідовності цифр, що зображують число.
Число одиниць будь-якого розряду, що об'єднуються в одиницю більше старшого розряду, називають підставою позиційної системи числення. Якщо кількість таких цифр одно P. то система числення називається P -ічной. Підстава системи числення збігається з кількістю цифр, використовуваних для запису чисел в цій системі числення.
Арифметичні дії над числами в будь-який позиційній системі числення виробляються за тими ж правилами, що і десятковій системі, так як всі вони грунтуються на правилах виконання дій над відповідними многочленами. При цьому потрібно тільки користуватися тими таблицями додавання і множення, які відповідають даній підставі P системи числення.
При додаванні цифри підсумовуються за розрядами, і якщо при цьому виникає надлишок, то він переноситься вліво.

В и ч и т а н і е
У м н о ж е н і е
Виконуючи множення багатозначних чисел в різних позиційних системах числення. можна використовувати звичайний алгоритм множення чисел в стовпчик, але при цьому результати множення і складання однозначних чисел необхідно запозичувати з відповідних даній системі таблиць множення і складання.
Множення в двійковій системі
Розподіл в будь-який позиційній системі числення проводиться за тими ж правилами, як і поділ кутом в десятковій системі. У двійковій системі розподіл виконується особливо просто, адже чергова цифра приватного може бути тільки нулем або одиницею. Приклад 9. Розділимо число 30 на число 6.
: 30. 6 = 510 = 1012 = 58.
Для переведення цілого десяткового чіслаNв систему числення з основаніемqнеобходімоNразделіть із залишком ( "без остачі") наq. записане в тій же десятковій системі. Потім неповну частку, отримане від такого поділу, потрібно знову розділити з залишком наq. і т.д. поки останнім отримане неповну частку не стане рівним нулю. Поданням чіслаNв новій системі числення буде послідовність залишків ділення, зображених однойq-ічной цифрою і записаних в порядку, зворотному порядку їх отримання.

5 Переклад чисел між різними системами числення: метод розкладання. [Призначення, порядок виконання операції переказу, принципи методу, застосування для перекладу чисел між довільними системами числення.]
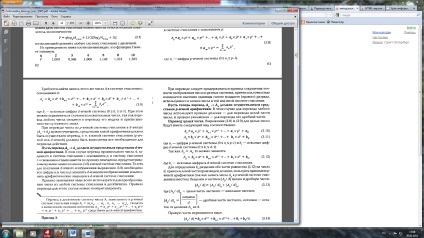
Переклад чисел між різними системами числення: табличний метод. [Призначення, порядок виконання операції переказу, принципи методу, застосування для систем числення, відмінних від двійковій.]
Табличний метод перекладу. У найпростішому вигляді табличний метод полягає в наступному: є таблиця всіх чисел однойсістеми з відповідними еквівалентами з другойсістеми; задача перекладу зводиться до знаходження відповідного рядка таблиці і вибору з неї еквівалента. Така таблиця дуже громіздка і вимагає великої ємності пам'яті для зберігання. Інший вид табличного методу полягає в тому, що є таблиці еквівалентів в каждойсістеме тільки для цифр цих систем і ступенів підстави (позитивних і негативних); задача перекладу зводиться до того, що в вираз ряду (3) для ісходнойсістемисчісленія треба підставити еквіваленти з новойсістеми для всіх цифр і ступенів підстави і зробити відповідні дії (множення й додавання) за правилами q2 -аріфметікі. Отриманий результат цих дій буде ізображатьчісло в новойсістемесчісленія.
Це зручний, але довгий і громіздкий спосіб
Переклад дробових чисел (десятковий формат) між різними системами числення: метод розкладання. [Призначення, порядок виконання операції переказу, принципи методу, застосування для перекладу чисел між будь-якими системами числення.]
Переклад з недесяткових позиційної системи числення в десяткову здійснюється обчисленням значення полінома, що відповідає цьому числу. На першому етапі записуємо число у вигляді полінома, де підставу системи, з якої перекладається число, виражається в десятковій системі числення. На другому етапі обчислюється значення полінома за правилами десяткової арифметики.
Приклад: Перевести двійкове число 110110,1 в десяткову систему числення:
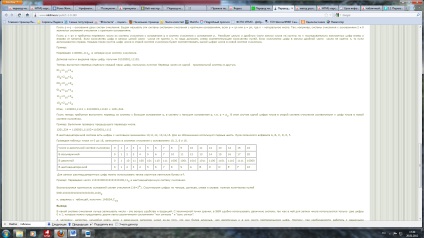
Для перекладу неправильної десяткового дробу в систему числення з недесяткових підставою необхідно окремо перевести цілу частину і окремо дробову.
Перекласти 23.12510 "2" с.с.
1) Переведемо цілу частину: