«Геометрія ножиць. Завдання на розрізування і складання фігур »
Федеральні державні освітні стандарти поставили на перше місце не предметний, а особистісний результат. На перший план виходять не так самі знання, скільки засоби і інструменти їх самостійного придбання, поглиблення та оновлення знань, незалежно від того, до якої предметної області вони належать.
Для вчителя робота по федеральним державним освітнім стандартам - це перехід від передачі знань до створення умов для активного пізнання і отримання дітьми практичного досвіду.
Для учнів це - перехід від пасивного засвоєння інформації до активного її пошуку, критичного осмислення, використання на практиці.
Важко не погодитися з тим, що геометричні завдання завжди викликають в учнів найбільші труднощі. Як результат - багато випускників погано вирішують завдання модуля «Геометрія» на підсумковій атестації. На мій погляд, причин такого становища можна виділити чимало, як суб'єктивних, так і об'єктивних. Ось деякі з них: слабка внутрішня (пізнавальна) мотивація, відсутність інтересу при вирішенні геометричних задач, невміння виділяти головне в завданні, погано розвинене просторове уявлення, відсутність розуміння зв'язку набутих знань, умінь і їх використання в практичній діяльності і ін. Мені здається, що велику допомогу у вирішенні цих проблем можуть надати завдання на побудову. Ці завдання зазвичай не допускають стандартного підходу до них і формального сприйняття їх учнями. Однак, цим завданням в шкільному курсі геометрії приділяється мало уваги і часу, в результаті все зводиться лише до розгляду найпростіших завдань на побудову, хоча, важливість конструктивних завдань у розвитку логічного мислення, естетичного виховання та прикладної спрямованості важко переоцінити. Ці завдання корисні і для розвитку просторового бачення, що необхідно при вивченні стереометрії в старших класах.
Тому, просто необхідно на позакласних заняттях розглядати завдання на побудову, додавши, в обов'язковому порядку, завдання на розрізування і складання фігур, а також завдання на картатій папері. Навіть ці, на перший погляд, нескладні завдання ставлять в тупик випускників, тому що вони не володіють прийомами вирішення завдань, у них недостатньо сформовані геометричні уявлення про площу і її властивості. Завдання на розрізування і складання, завдання на картатій папері покликані виправити ці недоліки, крім того, вони розвивають практичні навички, підвищують інтерес до геометрії і математики, розвивають фантазію, логіку, формують і вдосконалюють дослідницькі вміння і навички.
Наведу приклад одного з позакласних занять з геометрії, яке було проведено в 7 класі.
- знайомство учнів з різними завданнями на розрізання та складання фігур;
- знаходження площ фігур на картатій папері;
- формування просторової уяви учнів;
- активізації пошуково-пізнавальної діяльності учнів;
- розглянути різні способи вирішення геометричних завдань на розрізання та складання фігур на площині;
- познайомити з завданнями на картатій папері і їх рішенням;
- розвивати винахідливість і нестандартність мислення учнів;
- розвивати інтерес до практичного використання знань в конструюванні.
Подивіться на картини відомих і невідомих художників. Як ви думаєте, що їх об'єднує?






Спробуйте пофантазувати і припустити, рішенням яких завдань можуть бути зайняті персонажі картин? Можливо, що вони вирішують завдання на побудову. А нам знайомі такі завдання? Які інструменти можна використовувати при вирішенні класичних завдань на побудову?
Але ми сьогодні будемо вирішувати дещо інші завдання. А що це за завдання, здогадайтеся самі. Відомо, що з цими завданнями, очевидно, зіткнувся ще первісна людина, коли намагався розкроїти шкуру вбитого звіра, щоб зшити собі одяг. Рішення багатьох простих подібних завдань були знайдені ще древніми греками. Здогадалися, про які завданнях йдеться?
Так, звичайно, мова йде про завдання на розрізування. Завдання на розрізування або на перекроювання фігур виникли в далекій давнині. Уже в VII-- ст. до н.е. в Індії в книзі «Правила мотузки» розглядаються завдання на перекроювання фігури, що складається з двох квадратів, в рівновеликий їй квадрат і перекроювання прямокутника в квадрат. Перший письмовий джерело з подібними завданнями відноситься до Х століття - це фрагменти трактату перського астронома Абул-Вефа, що жив в Багдаді. Професійні математики всерйоз зайнялися завданнями на розрізання ближче до середини XIX століття.
Відкладемо в сторону циркуль і візьмемо ножиці. Кроїти, вирізати, міркувати - ось що потрібно при вирішенні завдань з геометрії ножиць.
Завдання на розрізування і перекроювання фігур.
Перекроїти фігуру, що складається з двох квадратів, в рівновеликий їй квадрат.
(Для вирішення завдання хлопцям треба знайти відповідь на питання: які фігури є рівновеликими? Вони знаходять відповідь або в математичному довіднику, або в інтернеті).
Рішення. Розрізати по діагоналі кожен квадрат. Діагоналі будуть сторонами отриманого квадрата.
Розріжте прямокутник, довжина якого дорівнює 9 клітин, а ширина 4, на дві рівні частини так, щоб з них можна було скласти квадрат.
Побудуйте прямокутник зі сторонами 2 см і 5 см. Розріжте прямокутник по діагоналі. Складіть з вийшов частин трикутник.
Чи можна з цих частин скласти ще один трикутник, що не рівний даному? Якщо можна, то складіть ще один трикутник.
Побудуйте прямокутний трикутник, у якого дві сторони рівні. Розріжте його на три нерівні частини, з яких можна було б скласти два рівних квадрата.
Розріжте квадрат на 3 частини, з яких можна скласти трикутник з 3 гострими кутами і трьома різними сторонами.
Рішення представлено на малюнку.
Завдання на знаходження площі фігури на картатій папері.
Випускники здають ЄДІ, який передбачає вирішення цікавих, нестандартних завдань з курсу геометрії. Багато з них можна вирішити, не використовуючи формули, а застосовуючи метод розрізання і перекроювання. Розглянемо одну таку задачу.
Завдання №5. Знайдіть площу трапеції, зображеної на картатій папері з розміром клітини 1 см × 1 см (див. Рис.). Відповідь дайте у квадратних сантиметрах.
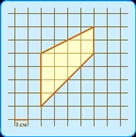
Хлопці спочатку пропонують свої рішення.
А тепер пропоную розглянути один із способів вирішення. Ви не знаєте формули знаходження площі трапеції, але володієте хорошим уявою. Спосіб те саме рішення головоломки - як розрізати плоску фігуру на частини, щоб з цих частин, використовуючи кожну з них однакове число раз, скласти прямокутник? Потім, просто порахувати кількість клітинок усередині прямокутника, і розділити на число повторів деталей заданої фігури. Дивіться.
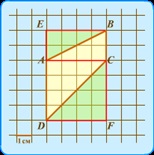
Проводимо додаткову лінію AC і «розрізаємо» трапецію на дві частини, як у вирішенні другим способом. Проводимо додаткові лінії і будуємо вершини E і F, як в рішенні третім способом. Переконуємося в тому, що отримані зелені і жовті трикутники попарно рівні (підрахунком клітинок на відповідних сторонах). Значить, для побудови прямокутника деталі заданої фігури використані 2 рази, один комплект жовтий, другий - зелений. Вважаємо загальна кількість клітинок в закрашенном прямокутнику. Виходить 24. Ділимо на 2. 24/2 = 12. Відповідь: 12.
Розглянемо ще один спосіб вирішення завдання. Спосіб вимагає тих же самих знань, що і попередній, тільки трошки іншого погляду на картинку. Тепер ми будемо не «розрізати» нашу трапецію на частини, а «вирізати» її з прямокутника, сторони якого проходять по лініях сітки через вершини заданої трапеції.
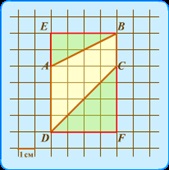
Проводимо горизонтальні лінії через вершини В і D, продовжуємо вертикальні лінії AD і ВС до перетину з горизонтальними. Точки перетину позначимо символами E і F. Отримали прямокутник DEBF зі сторонами DE = 6 і DF = 4, його площа 6 × 4 = 24. Щоб отримати шукану площу трапеції, потрібно з площі цього прямокутника відняти площі (зелених) трикутників AEB і DFC.
SAEB = AE · EB / 2 = 2 · 4/2 = 4 і SDFC = DF · FC / 2 = 4 · 4/2 = 8.
Отже, площа трапеції дорівнює S = 24 - 4 - 8 = 12.
Розгляньте завдання з відкритого банку завдань ЄДІ, запропонуйте їх вирішення.




Наше пригода добігає кінця. На наступному занятті ми продовжимо рішення задач на розрізання, перекроювання, знаходження площ фігур на картатій папері, додамо ще фігури на координатної площині. Я сподіваюся, що світ наочної геометрії вас захопив.
Пропоную вам до наступного заняття виконати одне із завдань:
- підберіть і вирішите завдання з відкритого банку завдань ЄДІ з математики на знаходження площ фігур, зображених на картатій папері.