Зображення називається повним, якщо воно допускає однозначне побудова зображення будь-інціденцій (взаємної приналежності), що має місце в оригіналі. Для досягнення позиційної повноти зображення в педагогічному процесі застосовується так званий метод основної площини.
У чому ж полягає цей метод?
У просторі фіксується деяка площину, яка називається основною площиною. Вибирається напрямок паралельного проектування - пряма а. перетинає дану площину.
Нехай ,, С - точки простору. Точки *, *, С * - їх проекції на площину. Це так зване внутрішнє проектування. Його легко змоделювати, використовуючи модель площині - деяку поверхню, в яку можна вставляти спиці, і спиці імітують проектують прямі.
Потім вибирається площину зображення, наприклад площину екрану або стіни, і напрямок зовнішнього проектування - промені проектора або сонця.
Виходить, що фігуру і її проекцію на площину з проектують прямими як би «фотографуємо», тобто відображаємо на площину зображення.
Покажемо, що метод основної площини (подвійне проектування) гарантує позиційну повноту зображення.
Так, по малюнку, на якому зображені точки К, Р, С і М. не можна сказати, як ці точки розташовані відносно площини. Нічого певного не можна стверджувати і про те, перетинає пряма КР дану площину.
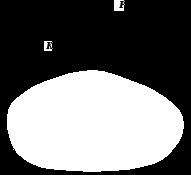
Для того, щоб можна було відповісти на подібні питання, скористаємося методом основної площини.
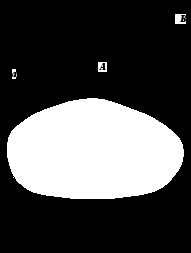
Разом з кожною точкою простору на зображенні вказано її основа - проекція на основну площину. З'ясуємо, як розташована пряма АВ відносно площини.
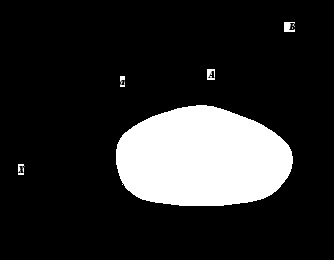
Проведемо пряму АВ і її проекцію АВ на основну площину до перетину. Точка Х - точка перетину прямої АВ з її проекцією на площину. Можна довести, що точка Х - точка перетину прямої АВ і площини.
Отже, пряма АВ перетинає площину.
Таким чином, точка вважається заданої на зображенні, якщо дано її підставу (проекція точки на основну площину).
Будь-яка пряма буде задана на зображенні, якщо задані підстави двох її точок (самі точки і їх проекції на основну площину).
Площина вважається заданою, якщо задані три точки площини, що не лежать на одній прямій, і їх проекції на основну площину.
Метод основний площині дійсно гарантує позиційну повноту зображення.
Для однозначного вирішення завдань на кресленнях корисно знати:
Зображення плоскої фігури завжди повне за умови, якщо воно не є виродженим. Основний площиною є площина самої фігури.
Зображення призми і циліндра завжди повне. Основна площину - площину підстави призми або циліндра, напрямок внутрішнього проектування паралельно бічному ребру призми (утворює циліндра).
Зображення піраміди і конуса завжди повне. Основна площину - площину підстави піраміди або конуса. В якості внутрішнього проектування виступає центральне проектування - центр знаходиться в вершині піраміди або конуса.
Зображення кулі в ортогональної проекції - повне.