Презентація на тему: "Циклоїда 1 Крива, яку описує точка, закріплена на кола, що котиться по прямій, називається циклоїдою. Для зображення циклоїди відкладемо на." - Транскрипт:
1 Циклоїда 1 Крива, яку описує точка, закріплена на кола, що котиться по прямій, називається циклоїдою. Для зображення циклоїди відкладемо на прямій відрізок АВ, що дорівнює довжині кола, тобто АВ = 2πR. Розділимо цей відрізок на 8 рівних частин точками А 1. А 8 = В. З'ясуйте, де буде знаходиться зазначена точка A, коли окружність, що котиться по прямій, досягне точки B?

2 Циклоїда 2 Де буде знаходиться зазначена точка A, коли окружність, що котиться по прямій, досягне точки: а) A 4; б) A 2; в) A 6; г) A 1; д) A 3; е) A 5; ж) A 7;? (Для вказівки положення точки використовуйте напрямки: схід, захід, північ, південь і т.д.) Відповідь: а) північ; б) захід; в) схід; г) південний захід; д) північний захід; е) північний схід; ж) південний схід.
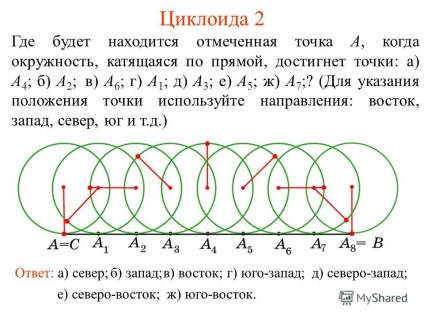
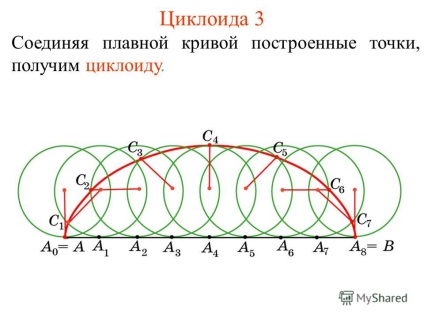
3 Циклоїда 3 Поєднуючи плавною кривою побудовані точки, отримаємо циклоиду.
4 Циклоїда в русі Першим, хто став вивчати циклоиду, був Галілео Галілей (1564 - 1642). Він же придумав і її назва.

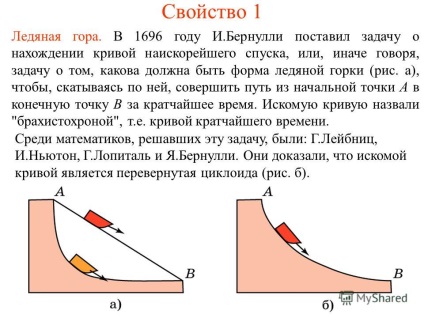
5 Властивість 1 Крижана гора. В 1696 И.Бернулли поставив завдання про знаходження кривої найшвидшого спуску, або, інакше кажучи, завдання про те, якою має бути форма крижаної гірки (рис. А), щоб, скочуючись по ній, зробити шлях з початкової точки А в кінцеву точку В за найкоротший час. Шукану криву назвали "брахістохрони", тобто кривої найкоротшого часу. Серед математиків, які вирішували це завдання, були: Г. Лейбніц, І. Ньютон, Г.Лопіталь і Я. Бернуллі. Вони довели, що шуканої кривої є перевернута циклоїда (рис. Б).
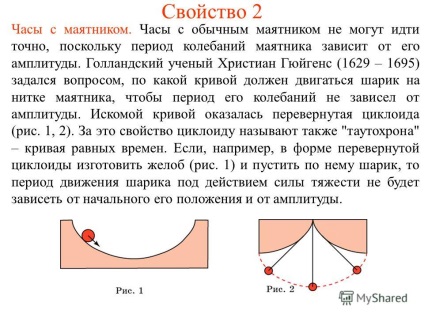
6 Властивість 2 Годинники з маятником. Годинники зі звичайним маятником не можуть йти точно, оскільки період коливань маятника залежить від його амплітуди. Голландський вчений Християн Гюйгенс (1629 - 1695) задався питанням, з якої кривої повинен рухатися кульку на нитці маятника, щоб період його коливань не залежав від амплітуди. Шуканої кривої виявилася перевернута циклоїда (рис. 1, 2). За це властивість циклоиду називають також "таутохронность" - крива рівних часів. Якщо, наприклад, у формі перевернутої циклоїди виготовити жолоб (рис. 1) і пустити по ньому кульку, то період руху кульки під дією сили тяжіння не буде залежати від початкового його положення і від амплітуди.
7 Вправа 1 Окружність радіуса 1 котиться по прямій. На якій відстані від цієї прямої будуть знаходиться точки C 1, ..., C 7. Відповідь. 1. 2. 1.

8 Вправа 2 Чи має циклоїда: а) осі симетрії; б) центр симетрії? Відповідь: а) Так; б) немає.
9 Подовжена циклоїда Крива, яку описує точка, закріплена на продовженні радіуса кола, що котиться по прямій, називається подовженою циклоїдою.
11 Укороченная циклоїда Крива, яку описує точка, закріплена на радіусі всередині кола, що котиться по прямій, називається скороченою циклоїдою.
13 Вправа 1 Намалюйте траєкторію руху вершини правильного трикутника, що котиться по прямій.
14 Вправа 2 Намалюйте траєкторію руху вершини квадрата, що котиться по прямій.
15 Вправа 3 Намалюйте траєкторію руху вершини правильного шестикутника, що котиться по прямій.
16 Кардіоїда 1 Траєкторія руху точки, закріпленої на кола, що котиться з зовнішньої сторони по іншій окружності того ж радіуса, називається кардіоїд. Відповідь: а) Захід; б) схід; в) схід; г) південь; д) північ; е) південь; ж) північ. Для зображення кардіоїди розділимо окружність на 8 рівних частин точками А 1. А 8 = В. З'ясуйте, де буде знаходитися зазначена точка A, коли окружність, що котиться по прямій, досягне точки: а) A 4; б) A 2; в) A 6; г) A 1; д) A 3; е) A 5; ж) A 7.
17 Кардіоїда 2 Поєднуючи плавною кривою побудовані точки, отримаємо кардиоиду.
18 Кардіоїда в русі
19 Вправа 1 Чи має кардіоїда: а) осі симетрії; б) центр симетрії? Відповідь: а) Так; б) немає.
20 Вправа 2 Намалюйте траєкторію руху вершини правильного трикутника, що котиться з зовнішньої сторони за іншим правильному трикутнику.
21 Вправа 3 Намалюйте траєкторію руху вершини квадрата, що котиться з зовнішньої сторони за іншим квадрату.
22 Вправа 4 Намалюйте траєкторію руху вершини правильного шестикутника, що котиться з зовнішньої сторони за іншим правильному шестикутнику.
23 Подовжена кардіоїда Траєкторія руху точки, закріпленої на продовженні радіуса кола, що котиться по іншій окружності того ж радіуса, називається подовженою кардіоїд. Намалюйте цю криву.
25 Укороченная кардіоїда Траєкторія руху точки, закріпленої на радіусі всередині кола, що котиться по іншій окружності того ж радіуса, називається скороченою кардіоїд. Намалюйте цю криву.
27 Астроіда Траєкторія руху точки, закріпленої на кола, що котиться всередині іншої окружності в 4 рази більшого радіусу, називається астроїда. Намалюйте цю криву.
29 Вправа 1 Чи має астроїда: а) осі симетрії; б) центр симетрії? Відповідь: а) Так; б) так.
30 Вправа 2 Намалюйте траєкторію руху вершини квадрата зі стороною 1, що котиться з внутрішньої сторони за іншим квадрату зі стороною 4.
31 Подовжена астроїда Траєкторія руху точки, закріпленої на продовженні радіуса кола, що котиться всередині іншої окружності в 4 рази більшого радіусу, називається подовженою астроїда. Намалюйте цю криву.
33 Крива Штейнера Траєкторія руху точки, закріпленої на кола, що котиться всередині іншої окружності в 3 рази більшого радіусу, називається кривою Штейнера. Намалюйте цю криву.
35 Подовжена крива Штейнера Траєкторія руху точки, закріпленої на продовженні радіуса кола, що котиться всередині іншої окружності в 3 рази більшого радіусу, називається подовженою кривої Штейнера. Намалюйте цю криву.
36 Подовжена крива Штейнера
37 епіциклоїда Крива, яку описує точка, закріплена на кола, що котиться з зовнішньої сторони по іншій окружності, називається епіциклоїда. При цьому відношення радіусів може бути різним. Намалюйте епіциклоїда в разі, коли відношення радіусів дорівнює 2: 3.
39 Подовжена епіциклоїда Крива, яку описує точка, закріплена на продовження радіусу кола, що котиться з зовнішньої сторони по іншій окружності, називається подовженою епіциклоїда. При цьому відношення радіусів може бути різним. Намалюйте подовжену епіциклоїда в разі, коли відношення радіусів дорівнює 2: 3.
41 Укороченная епіциклоїда Крива, яку описує точка, закріплена на радіусі кола, що котиться з зовнішньої сторони по іншій окружності, називається скороченою епіциклоїда. При цьому відношення радіусів може бути різним. Намалюйте укорочену епіциклоїда в разі, коли відношення радіусів дорівнює 2: 3.
43 гіпоциклоїда Крива, яку описує точка, закріплена на кола, що котиться з внутрішньої сторони по іншій окружності, називається гіпоциклоїда. При цьому відношення радіусів може бути різним. Намалюйте гіпоциклоїда, коли відношення радіусів дорівнює 2: 5.
45 Вправа 1 Намалюйте траєкторію руху точки, закріпленої на кола, що котиться з зовнішньої сторони по іншій окружності, якщо відношення радіусів дорівнює 1: 2.
46 Вправа 2 Намалюйте траєкторію руху точки, закріпленої на кола, що котиться з зовнішньої сторони по іншій окружності, якщо відношення радіусів дорівнює 2: 1.
47 Вправа 3 Намалюйте траєкторію руху точки, закріпленої на кола, що котиться з зовнішньої сторони по іншій окружності, якщо відношення радіусів дорівнює 2: 5.
48 Вправа 4 Намалюйте траєкторію руху точки, закріпленої на кола, що котиться всередині іншої окружності в два рази більшого радіусу. Крива в русі Відповідь: Діаметр кола.
49 Вправа 5 Доведіть, що траєкторією руху точки, закріпленої на кола, що котиться всередині іншої окружності в два рази більшого радіусу, є діаметр. Рішення: Нехай котиться коло перемістилася з точки B в точку D, P - її центр. Позначимо C точку перетину діаметра AB з цим колом. Тоді кут CPD в два рази більше кута BOD. Отже, дуги BD і CD рівні, тобто C - точка, закріплена на котиться кола.