Презентація на тему: "Функції Поняття функції Способи завдання функції Нулі функції Область позитивності і область отріцательності функції Зростання і спадання функції Екстремуми." - Транскрипт:
1 Функції Поняття функції Способи завдання функції Нулі функції Область позитивності і область отріцательності функції Зростання і спадання функції Екстремуми функції

2 Готфрід Вільгельм Лейбніц Німецький математик 1646 - 1716

3 Нулі функції Щоб знайти нулі функції y = f (x), потрібно вирішити рівняння f (x) = 0. Значення аргументу (x), при яких значення функції (y) рівні 0, називаються нулями функції.

4 Нулі функції Нулі функції - це точки осі абсцис (ОХ), в яких графік функції перетинає цю вісь. Безліч всіх нулів функції позначається символом Хо.

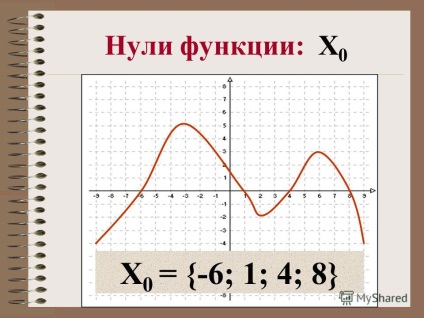
5 Нулі функції: X 0 X 0 =
0. Область позитивності функції - це безліч тих значень аргументу (х), при яких функція набуває додатних значень. "Title =" Область позитивності Щоб знайти область позитивності функції y = f (x), потрібно вирішити нерівність f (x)> 0. область позитивності функції - це безліч тих значень аргументу (х), при яких функція набуває додатних значень. "class =" link_thumb "> 6 область позитивності Щоб знайти область позитивності функції y = f (x), потрібно вирішити нерівність f (x)> 0. Область позитивності функції - це безліч т х значень аргументу (х), при яких функція набуває додатних значень. 0. Область позитивності функції - це безліч тих значень аргументу (х), при яких функція набуває додатних значень. "> 0. Область позитивності функції - це безліч тих значень аргументу ( х), при яких функція набуває додатних значень. "> 0. Область позитивності функції - це безліч тих значень аргументу (х), при яких функція набуває додатних значень." title = "Область позитивності Щоб знайти область позитивності функції y = f (x), потрібно вирішити нерівність f (x)> 0. Область позитивності функції - це безліч тих значень аргументу (х), при яких функція набуває додатних значень.">

0 X + = (-6; 1) (4; 8) "title =" Область позитивності: X + f (x)> 0 X + = (-6; 1) (4; 8) "class =" link_thumb " > 7 Область позитивності: X + f (x)> 0 X + = (-6; 1) (4; 8) 0 X + = (-6; 1) (4; 8) "> 0 X + = (- 6; 1) (4; 8) "> 0 X + = (-6; 1) (4; 8)" title = "Область позитивності: X + f (x)> 0 X + = (-6; 1) (4; 8) "> 0 X + = (-6; 1) (4; 8)" title = "Область позитивності: X + f (x)> 0 X + = (-6; 1) (4; 8 ) ">
8 Область отріцательності Щоб знайти область отріцательності функції y = f (x), потрібно вирішити нерівність f (x)
9 Область отріцательності: X - f (x)
10 Вирішуємо 207 (1, 2) 208 (1, 2, 4)
x 1, то f (x 2)> f (x 1). "title =" Зростання функції Функція y = f (x) називається зростаючою на інтервалі (a; b), якщо на цьому інтервалі більшому значенню аргументу відповідає більше значення функції , т. е. якщо x 2> x 1, то f (x 2)> f (x 1). "class =" link_thumb "> 11 Зростання функції Функція y = f (x) називається зростаючою на інтервалі (a; b ), якщо на цьому інтервалі більшому значенню аргументу відповідає більше значення функції, т. е. якщо x 2> x 1, то f (x 2)> f (x 1). x 1, то f (x 2)> f ( x 1). "> x 1, то f (x 2)> f (x 1)."> x 1, то f (x 2)> f (x 1). " title = "Зростання функції Функція y = f (x) називається зростаючою на інтервалі (a; b), якщо на цьому інтервалі більшому значенню аргументу відповідає більше значення функції, т. е. якщо x 2> x 1, то f (x 2 )> f (x 1). "> x 1, то f (x 2)> f (x 1)." title = "Зростання функції Функція y = f (x) називається зростаючою на інтервалі (a; b), якщо на цьому інтервалі більшому значенню аргументу відповідає більше значення функції, т. е. якщо x 2> x 1, то f (x 2)> f (x 1). ">
12 Зростання функції: X X = (-; -3) (2; 6)
x 1, то f (x 2) x 1, то f (x 2) 13 Зменшення функції Функція y = f (x) називається спадною на інтервалі (a; b), якщо на цьому інтервалі більшому значенню аргументу відповідає менше значення функції, т. е. якщо x 2> x 1, то f (x 2) x 1, то f (x 2) x 1, то f (x 2) x 1, то f (x 2) x 1, то f ( x 2) x 1, то f (x 2) x 1, то f (x 2)
14 Зменшення функції: X X = (-3; 2) (6;)
15 Зростання і спадання функції Функція називається спадною, якщо її інтервалом убування є вся область визначення. Функція називається зростаючою, якщо її інтервалом зростання є вся область визначення.
16 Максимум функції: X max X max = -3; X max = 6
17 Мінімум функції Функція y = f (x) має мінімум в точці x 0, якщо знайдеться така околиця точки x 0, що для всіх значень аргументу х з цієї околиці виконується нерівність f (x 0)
18 Мінімум функції: X min X min = 2
19 Екстремуми функції Точки мінімуму і максимуму називаються точками екстремуму, а значення функції в цих точках - екстремумами функції.
20 Точки екстремуму: X е X е =
21 X = (-;) Y = (-;) X 0 = <0 ; 3>X + = (3;) X - = (-; 0) (0; 3) X = (-; 0) (2;) X = (0; 2) X е = <0 ; 2>max (0; 0), min (2; -4)
22