Під фінансовою операцією розуміють будь-які операції з вкладення, розміщення, інвестування тимчасово вільних грошових коштів або їх еквівалентів з метою отримання доходу.
Особа, яка надає тимчасово вільні кошти є кредитором. Особа, яка вчиняє фінансові операції з цими коштами і бере на себе зобов'язання повернути через певний час t ці кошти, збільшені на обумовлену суму доходу, називають позичальником.
Позначимо початкову суму розміщуються кредитором коштів через S0. а суму, що повертається позичальником після скоєння фінансової операції через де - величина доходу, отриманого від використання початкової суми протягом часу t.
Прибутковість фінансової операції можна визначити відношенням:
Прибутковість фінансової операції оцінюють в відносних величинах (1.1) або у відсотках:
Сума грошових коштів, що отримується кредитором в кінці фінансової операції, буде дорівнює де - дохідність у відносних одиницях.
При прийнятті рішення про вкладення тимчасово вільних грошових коштів кредитор враховує час t. через яке він отримає їх з доходом; прибутковість фінансової операції, яку обіцяє позичальник; можливі ризики, пов'язані з цією операцією.
Природно кредитор буде розглядати кілька варіантів фінансових операцій, серед яких буде практично безризикові розміщення грошових коштів на банківський депозит з гарантованою річною прибутковістю t = 1 рік.
Позначимо річну прибутковість по банківських депозитних внесках буквою i.
де і - величина доходу, і загальна сума отримується кредитором після закінчення одного року вкладу.
Величину i називають річною процентною ставкою - це сума, яка виплачується кредитору в кінці періоду нарахування 1 рік за кожну одиничну суму (наприклад, тис. Руб.) Зайняту позичальником на початку періоду.
Схема нарахування простих відсотків пояснюється рис. 1.1.
Мал. 1.1. Схема нарахування простих відсотків
Нехай початкова сума, внесена на депозит, дорівнює при річній процентній ставці i. Тоді нарощена за рік сума буде дорівнює:
Якщо депозитний договір укладено на n-років з фіксованою річною процентною ставкою, при нарахуванні доходу за схемою простих відсотків, то в кінці кожного року цей дохід переводиться на поточний рахунок, а сума, розміщена на депозиті, залишається постійною рівною.
На поточному рахунку банківська процентна ставка дорівнює нулю Доходи, що перераховуються на поточний рахунок, можуть на розсуд кредитора або залишатися на поточному рахунку або вилучатися для своїх потреб.
Якщо депозитний договір укладено на n-років, то в кінці терміну вкладу кредитор отримає суму:
При постійній річній процентній ставці і кінцева нарощена за n-років сума буде дорівнює:
Якщо процентна ставка змінюється рік від року, то:
де - річна процентна ставка в k -тому році.
Якщо момент повернення позики є змінною величиною (наприклад, депозитний вклад довостребованія), то нарощена сума в день видачі позики визначається за формулою:
де - день вкладення коштів на депозит;
- день повернення коштів;
- термін дії депозитного договору в днях;
- кількість днів в році.
Якщо грошові кошти в сумі за схемою простих відсотків послідовно вкладаються на проміжки часу днів з різними річними відсотковими ставками. то нарощена сума за весь період часу буде дорівнює:
Іноді депозитні договори укладаються з m-кратної нарахуванням відсотків на рік. При. відсотки нараховуються і можуть бути виплачені щоквартально, при - щомісяця. В цьому випадку нарощена сума на першому терміні виплати відсотків буде дорівнює:
де m - кратність нарахування відсотків на рік; i - річна процентна ставка.
Тоді при терміні вкладу 1 рік відсотки в розмірі будуть нараховані m раз, і нарощена сума по закінчення року дорівнюватиме:
Звідси випливає, що при розміщенні коштів за схемою простих відсотків збільшення кратності виплат не призводить до збільшення нарощеної суми.
Відповідно до формули (1.4) нарощена сума в схемі простих відсотків є лінійної зростаючою функцією зі збільшенням терміну вкладу (див. Рис. 1.3).
Отримання нарощеної суми при нарахуванні відсотків за схемою складних відсотків пояснюється рис. 1.2.
Мал. 1.2. Нарощення суми вкладу за схемою складних відсотків
При нарощенні за схемою складних відсотків відбувається реінвестування, або капіталізація отриманих відсотків. Припустимо, грошові кошти вкладаються в банк на депозитний договір з капіталізацією відсотків, що нараховуються по річній процентній ставці i на n-років.
Після закінчення першого року нарощена сума буде дорівнює:
На другому році сума депозитного вкладу дорівнюватиме і нарощена сума по закінченню другого року дорівнюватиме:
До кінця n-го року дії депозитного договору нарощена сума буде визначатися формулою:
Таким чином, послідовність нарощених сум є геометричною прогресією з початковим членом і знаменником прогресії Коефіцієнт пропорційності між нарощеної і первісною сумами називається коефіцієнтом нарощення. При визначенні нарощеної суми в довільний момент часу t необхідно користуватися формулою:
де - день вкладення грошових коштів на депозит;
- день закінчення депозитного договору;
- термін депозитного вкладу в днях;
- кількість днів в році.
Сумарний дохід. одержуваний за весь термін депозитного вкладу відповідно до формулами (1.6) і (1.7) може бути представлений у вигляді:
Визначимо нарощену суму при m-кратної нарахуванні відсотків на рік. Якщо нарахування складних відсотків відбувається m-раз на рік, то нарощена сума при першому нарахуванні відсотків буде дорівнює:
При другому нарахуванні відсотків:
Після закінчення одного року при m -тому нарахуванні відсотків нарощена сума буде дорівнює:
Якщо депозитний договір з m-кратної нарахуванням відсотків і їх капіталізацією полягає на n- років, то нарощену суму можна визначити за формулою:
Визначимо ефективну річну процентну ставку при m-кратної нарахуванні відсотків з їх капіталізацією з рівності одержуваних за рік нарощених сум:
Звідси для річної ефективної процентної ставки отримаємо:
Тоді формулу (1.10) для терміну депозитного договору на n-років при m-кратної нарахуванні відсотків можна записати у вигляді:
де - визначається формулою (1.11).
Відповідно до формулами (1.6), (1.7) і (1.12) нарощена сума в схемі складних відсотків є показовою функцією. Порівняння нарощених сум обчислюються за схемою простих та складних відсотків (див. Рис. 1.3) дозволяє зробити наступні висновки:
1) при терміні вкладу один рік нарощення за схемою простих та складних відсотків при однакових процентних ставках мають однаковий коефіцієнт нарощення;
2) при терміні вкладу менше одного року коефіцієнт нарощення за схемою простих відсотків більше ніж за схемою складних відсотків;
3) при терміні вкладу більше одного року коефіцієнт нарощення за схемою складних відсотків більше ніж за схемою простих відсотків;
4) при нарощенні за схемою складних відсотків m -кратноє нарахування відсотків призводить до збільшення коефіцієнта нарощення;
5) при нарощенні за схемою простих відсотків m -кратноє нарахування відсотків не впливає на коефіцієнт нарощення.
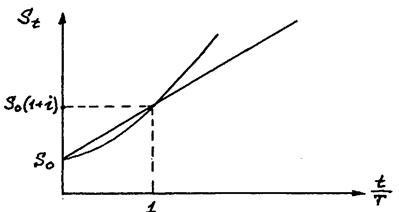
Мал. 1.3. Нарощення за простою і складною ставками