Статичну характеристику регулятора уявімо, як:
В даному випадку + С - швидкість вала виконуючого органу для зменшення потужності, що підводиться до печі; - С - швидкість вала для збільшення потужності, що підводиться.
Продифференцируем рівняння (3.3.) І підставивши значення dx / dt. отримаємо рівняння, що описують процес системи регулювання температури при різних положеннях контактів реле:
Побудуємо фазову траєкторію в фазовій площині з координатами х = q іh = dq / dt. Згідно зі слів (3.4.), Якщо dq / dt> 0 контакти регулятора переключаться при q = + b (лінія EF на ріс.96, б), якщо dq / dt <0 . то регулятор переключится при q = –b (линия GH), как изображено на рисунке 96.
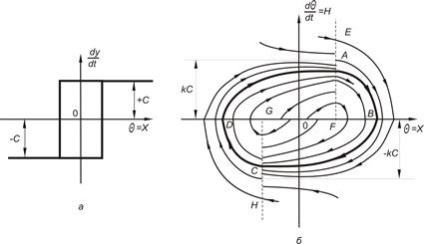
Ріс.96. Графічне представлення:
а) статичної характеристики регулятора
б) фазового портрета системи регулювання температури печі
Праворуч від ламаної EFGH на малюнку 96 фазовий портрет задовольняє умовам рівняння (3.5.), А зліва від ламаної EFGH умов рівняння (3.6.). Замінимо в рівнянні (3.5.) Dt = dq / h і отримаємо диференціальне рівняння фазових траєкторій:
Після інтегрування (3.7.) Отримаємо:
Подібним чином отримаємо диференціальне рівняння фазових траєкторій зліва від ламаної EFGH, яке матиме вигляд:
Криві на фазової площині, що утворюють фазовий портрет, являють собою фазові траєкторії при різних значеннях С1 ИС2. ці значення визначаються початковими умовами. Вид фазового портрета характеризує перехідний процес в нелінійної системі. У нашому випадку в системі характеризується незатухающими коливаннями температури, тому що в фазовому портреті є замкнутий контур ABCD, виділений жирною лінією, до якого сходяться фазові траєкторії.
Нелінійні системи можуть характеризуватися сталими станами рівноваги, що виникають в них після закінчення перехідних процесів, і періодичними процесами, які називали автоколиваннями. Нелінійні системи можуть мати кілька станів рівноваги. Автоколебания виникають за рахунок властивостей системи і не залежать від зміни зовнішнього впливу. Лінійні системи відрізняються від нелінійних систем можливістю наявності у останніх декількох станів рівноваги і можливістю виникнення автоколивань. Насправді розглядаються тільки стійкі стану рівноваги і автоколивання, причому стійкість одних не виключає нестійкості інших.
Від значення відхилення нелінійної системи від стану рівноваги може залежати її стійкість, при цьому розрізняють стійкість в «цілому», в «великому» і в «малому». Стійкість системи в «малому» характеризується стійкістю системи при малому відхиленні від стану рівноваги. Стійкість системи в «великому» говорить про стійкість системи при великому відхиленні. Система може бути стійка в «малому» і нестійка в «великому». Система вважається стійкою в «цілому» при будь-яких відхиленнях.
Аналіз фазових портретів дає можливість охарактеризувати особливості стійкості та виникнення автоколивань. На малюнку 97, а представлений фазовий портрет системи, яка при будь-якому початковому значенні х прийде в стан рівноваги (фазові траєкторії наближаються до початку координат). Про стан рівноваги дозволяє судити відрізок на осі абсцис, до якого сходяться фазові траєкторії, і розмір якого залежить від величини області нечутливості. Така система вважається стійкою в «цілому». На рис. 97, б зображений фазовий портрет системи, стійкої в «малому» і нестійкою в «великому». Даний висновок можна зробити на підставі того, що при малих початкових значеннях х фазові траєкторії сходяться до початку координат, а при великих значеннях х розходяться. Замкнутий контур фазового траєкторії розмежовує стійкість системи в «малому» від нестійкості в «великому» і називається нестійким періодичним режимом або граничним циклом.
В даному випадку наявність граничного циклу і напрямок фазових траєкторій від замкнутого контуру вказує на неможливість виникнення стійких автоколивань, тому що коливання будуть затухати або розходитися.
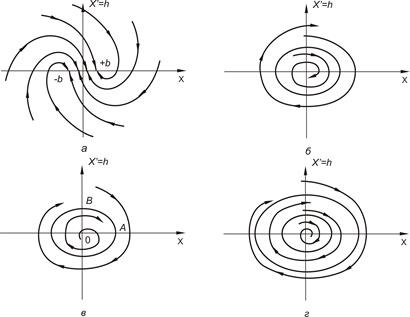
Ріс.97. Фазові портрети нелінійних систем управління:
а - система з областю нечутливості (-b ... + b), стійка в «цілому»,
б - система, стійка в «малому» і нестійка в «великому»,
в - система зі сталими автоколиваннями,
г - система з двома граничними циклами на фазової площині.
На малюнку 97, в, на фазовому портреті видно наявність розходиться до певних значень процесу при малому відхиленні системи від стану рівноваги. Має місце нестійкість системи в «малому», але при цьому амплітуда коливань збільшується тільки до певного значення, після якого залишається постійною, що говорить про виникнення стійких автоколивань. Замкнута фазова траєкторія, до якої спрямовані інші фазові траєкторії, говорить про наявність стійкого граничного циклу. Отже, при будь-якому значенні х в системі виникнуть автоколивання.
На малюнку 97, г фазовий портрет характеризує складнішу систему. На даному фазовому портреті зображені два замкнутих контуру, що вказують на існування періодичних режимів. Внутрішній граничний контур нестійкий і є кордоном стійкості в «малому». Зовнішній граничний контур стійкий і вказує на можливість виникнення стійких автоколивань в системі.
Параметри автоколебаний визначаються по замкнутому контуру. Наприклад, при гармонійних автоколиваннях, описуваних синусоїдою х = А sin wt. амплітуду автоколивань можна визначити, як довжину відрізка ОА на осі абсцис на малюнку 97, в. На підставі того, що х '= А cos wt. при cos wt = 1. відрізок ОВ дорівнює аw. тому частота автоколивань w = ОВ / ОА.
Насправді причина появи автоколивань пояснюється заздалегідь заданими перемиканнями в системі. На відміну від незатухаючих коливань автоколивання не характеризує синусоїдою, і їх фазова траєкторія не має форму еліпса, тому розрахунок зроблений з припущеннями.
З урахуванням вищесказаного сформулюємо відмінності стійкості нелінійних систем від стійкості лінійних систем:
- стійка «в цілому» нелінійна система може мати декілька станів рівноваги, лінійна система - одне;
- стійкість лінійних систем не залежить від величини початкового відхилення від стану рівноваги або, тоді як стійкість нелінійних систем - залежить;
- у нелінійних систем розрізняють стійкість в «цілому», в «великому» і в «малому», у лінійних систем подібна класифікація відсутня;
- у стійких нелінійних систем може існувати режим автоколивань, у лінійних систем - немає.