Нижче наведені деякі приклади побудов в прямокутних ізометричної і діметріческой проекціях.
I. Проекція сфери. На рис. 473 зверху дано зображення сфери в ізометричної і діметріческой проекціях.
В обох випадках сфера показана з вирізом однієї восьмої частини. Кола, що представляють собою нарис проекції, проведені: для ізометричної проекції радіусом, рівним
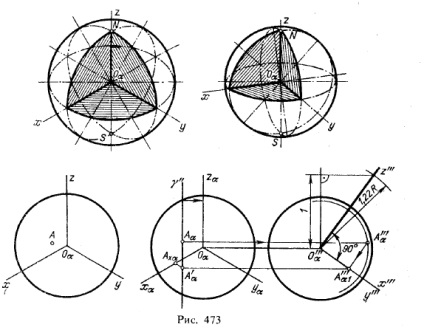
1,22R, для діметріческой проекції радіусом 1,06R, де R - радіус сфери. Еліпси в обох випадках відповідають екваторіальному і двом меридіональним перетинах.
На рис, 473 внизу зліва дано зображення сфери в ізометричної проекції; на видимій стороні сфери дана точка А. Справа показано побудова вторинної проекції А'α (див, рис, 449) і триланкової координатної ламаної лінії Аα А'α Ахα Оα. що дає можливість визначити прямокутні координати точки А в просторі. Побудова виконано в припущенні, що площину изометрических проекцій займає фронтальне положення і що равнонаклоненнью до неї осі х, у, z прямокутних координат спроектовані не тільки на цю площину, а й на додаткову профільну площину π3. Виходить система площин проекцій α, π3 і проекції Аα і А ' "α заданої точки А, причому А'" α отримана за допомогою перетину сфери пл. γ. Вторинна проекція точки А також зображена двома проекціями: А ' "α1 і А'α
2. Лінії перетину циліндра і конуса площиною. На рис, 474 і 475 показано побудову в ізометричної проекції ліній перетину циліндра і конуса фронтально-проектує площинами 1). У розглянутих випадках лінії перетину є еліпси.
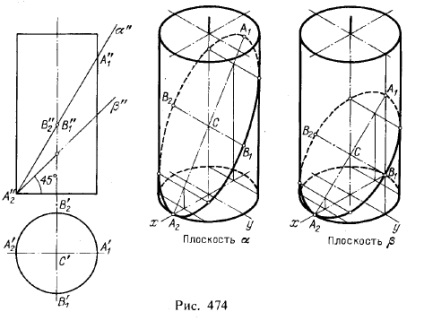
Перш за все, керуючись кресленням, наносимо за координатами точок А1 і А2 лінії нахилу ллоскостей α і β. Для побудови точок еліпсів беремо допоміжні січні площини: для циліндра - паралельно його утворюючим і площині yOz, для конуса - про-
1) Побудова виконано в наведених коефіцієнтах спотворення.
ходять через його вершину паралельно осі у. Ці площини задаються їх слідами, паралельними осі у, на площинах підстав циліндра і конуса.
При такому виборі допоміжних площин прямі, за якими вони перетинаються з площинами α і β, виходять паралельними осі γ. У перетині цих прямих з утворюють циліндра і конуса виходять точки еліпса.
В першу чергу слід знайти такі характерні точки, як відмічені на кресленнях буквами А1. А2. В1 і В2. а також одержувані на нарисових лініях ізометричної проекції. Мала піввісь одержуваного в перерізі еліпса, що дорівнює С'В'1. зберігає свою величину і в ізометричної проекції (С'В'1 = СВ1). Але своє значення малої осі для еліпса в ізометричної проекції відрізок В1 В2 зберігає лише при пл. β, т. е. при зазначеному на малюнку куті нахилу цієї площини, що дорівнює 45 °.
Дійсно, в цьому випадку відрізок В1 В2 будучи паралельним осі у, залишається і в ізометричної проекції перпендикулярним до A1 A2. отже, відрізки A1 A2 і В1 В2 зберігають своє значення осей еліпса. У разі ж іншого нахилу площини, як це показано на циліндрі для пл. α, відрізки А1 А2 і В1 В2 в ізометричної проекції не є осями еліпса, а лише його сполученими діаметрами.
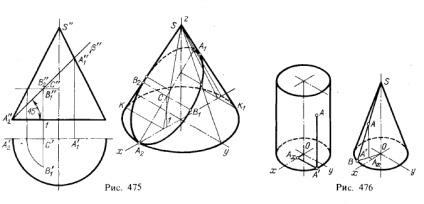
3. Побудова координатних відрізків для точки, заданої на поверхні циліндра і конуса обертання в аксонометрической проекції. На рис. 476 наведено приклади для циліндра і конуса в ізометричної проекції. У всіх випадках початок координат взято в центрі підстави (точка О).
Через задану на циліндрі точку А проведена пряма паралельно осі z, і з вторинної проекції А 'проведена пряма шраллельно осі γ до перетину з віссю х. Відрізки 0Аx. Аx А 'і А'А дозволяють визначити координати точки А в даній системі осей координат.
Через задану на конусі точку А проведена утворює і побудована вторинна проекція (ОВ) цієї утворює. Проводячи з точки А перпендикуляр до перетину з ОВ, отримуємо вторинну проекцію точки А. Подальше ясно з креслення.
На рис. 477 показано побудову координатних відрізків для точки, заданої на поверхні усіченого конуса обертання в ізометричної проекції (рис. 411, а). Покладемо, що ми маємо перетин конуса площиною, що проходить через вісь
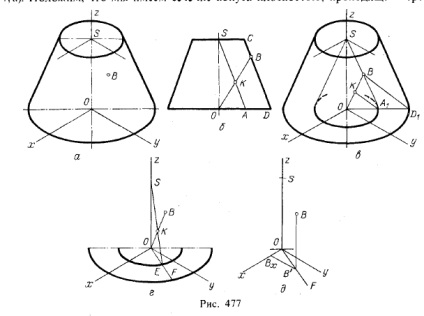
конуса і точку В (рис. 477,6). В отриманій трапеції проведена пряма SA || CD і перетинає її в точці К пряма ОВ. Отримуємо OK. KB = OA. AD. Але ця пропорція збережеться в ізометричної проекції. Побудуємо конус з вершиною в точці S і з котра утворює, паралельної утворює усіченого конуса (рис. 477, в). від
носіння OA1. A1 D1 повторює ставлення OA. AD, що міститься у зазначеній вище пропорції. Тепер можна отримати точку К на ОВ на рис. 477, ст. Утворює, проведена через точки S і Е, визначає точку К (рис. 477, г) і проекцію OF утворює, на якій знаходиться точка В. Звідси ми отримуємо можливість отримати вторинну проекцію В '(рис. 477, д) і координатні відрізки ВВ ', В'Вx і ОВХ. визначають координати z, у і х.
Зазначене побудова дається на випадок, якщо не можна добудувати усічений конус до повного. Якщо добудувати можна, то побудова проводиться, як показано для конуса на рис. 477,6.
4. Приклади побудови ліній перетину циліндричних і конічних поверхонь обертання між собою. Лінії перетину будують по точках; ці точки знаходять або за їх координатами, узятим з ортогональних проекцій, або способом допоміжних січних площин безпосередньо в аксонометричних проекціях. Останнє показано на рис. 478, а - р
Допоміжні січні площині перетинають дані циліндри і конуси по утворюючим лініях. На рис; 478, а осі циліндрів перетинаються, на рис. б) схрещуються. Якщо на рис. а) точки А і А1 визначалися за допомогою січної площини, що проходить через осі обох циліндрів, то на рис. б) треба врахувати зсув на
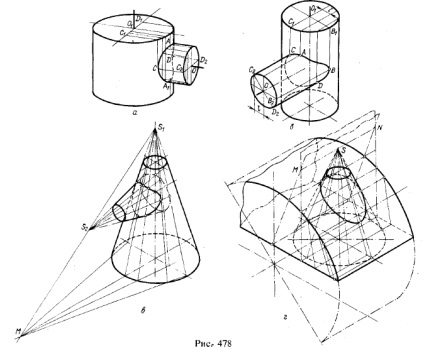
l 1). На рис. 478, в січні площині проходять через пряму S1 S2. а їх сліди на площині основи конуса з вершиною S1 проходять через слід прямий S1 S2 на цій площині. На рис. 478, г площині проходять через пряму MN, проведену через вершину конуса - точку S - паралельно твірної циліндра.
1) Розмітка точок буквами проведена лише для пояснення.
5. Побудова точок дотику кола - нарису проекції сфери - з еліпсом - проекцією окружності, одержуваної на сфері при перетині її площиною. На рис. 479, а показана сфера, зрізана трьома площинами - профільної (γ), горизонтальної (δ) і фронтально-проецирующей (β). З цього кресленням побудована: ізометрична проекція (рис. 479,6) в наведених коефіцієнтах спотворення. Еліпс m побудований так, як було показано на рис. 469, а еліпс n - як на рис. 465. Проекція сфери дана нарисом - окружністю радіуса рівного 1,22R. Ця окружність стосується еліпса m в точці К, еліпса n - в точці L.
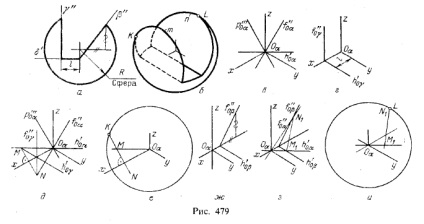
Розглянемо, як знайдена точка К. Вона отримана на окружності - нарисі проекції сфери, т. Е. В площині ізометричної проекції (α), і в той же час на еліпсі m т. Е. В пл. γ, що перетинає сферу. Але якщо точка належить одночасно двох площинах, то вона належить лінії перетину цих площин.
Площина ізометричної проекції, як відомо, равнонаклонна до π1. π2 і π3. Трикутник слідів цієї площини рівносторонній (див. Рис. 457). Віднісши пл. α до точки Оα. т. е. до початку осей і центру сфери, помучити положення слідів, вказане на рис. 479, ст.
Пл. γ в системі тих же осей відіб'ється в слідах, як показано на рис. 479, м. Сумісний рис. в) і г) і побудуємо лінію перетину площин α і γ (рис. 479, е): пряма MN проходить через точку M перетину горизонтальних слідів паралельно сліду р " '0α. так як γ || π3 (при цьому р"' 0α ⊥Oα X. отже, MN⊥Оα х).
Тепер залишається знайти точку До в перетині прямої MN з окружністю - ізометричної проекцією сфери (рис. 479, е).
Для визначення положення точки L (див. Рис. 479, б) треба зобразити в системі изометрических осей фронтально-проецирующую пл. β (рис. 479, .ж), а потім знайти пряму перетину площин α і β (рис. 479, з), ця пряма проходить через точку M1 перетину слідів h'0β і h'0α і через точку N1 перетину слідів f " 0β і f "0α. Шукана точка L виходить в перетині прямої M1 N1 з окружністю - ізометричної проекцією сфери (рис. 479, і).