Приклад 1. Вирішити систему рівнянь методом Крамера
Складемо і обчислимо спочатку головний визначник цієї системи:
Так як, то система має єдине рішення, яке можна знайти за правилом Крамера:
де виходять з визначника шляхом заміни 1-го, 2-го або 3-го стовпця, відповідно, на стовпець вільних членів.
Отже, - єдине рішення.
Приклад 2. Вирішити систему рівнянь методом Крамера
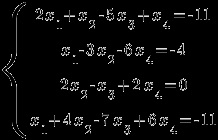
Складемо головний визначник цієї системи:
Використовуючи властивості визначника, створимо в першому стовпці нулі. Для цього
- Другий і третій рядок залишимо без изменеий,
- Помножимо другий рядок на -2 і додамо до першої
- Помножимо другий рядок на -1 і додамо до четвертої
Після цих перетворень значення визначника не зміниться, але він набере такого вигляду
Тепер, скориставшись визначенням визначника і розклавши його по елементах четвертого стовпця, отримаємо:
Отже, головний визначник системи рівнянь відмінний від нуля. За правилом Крамера така система має єдине рішення. Знайдемо його. Для цього створимо і обчислимо ще чотири визначники:
За правилом Крамера маємо рішення:
Отже, - єдине рішення.