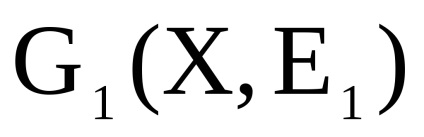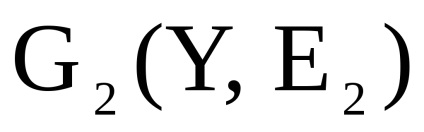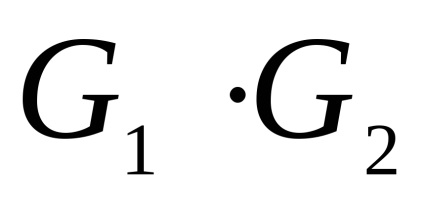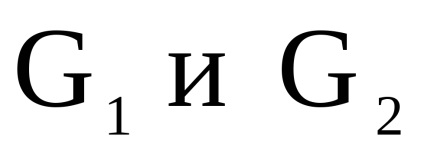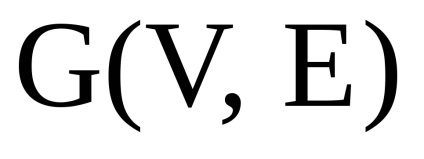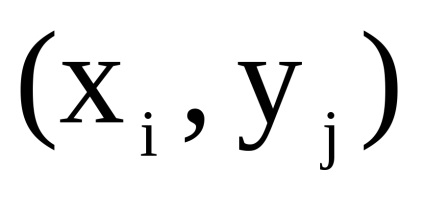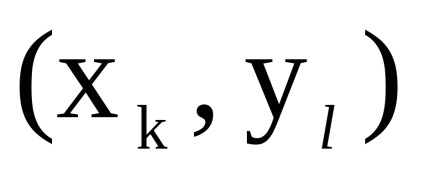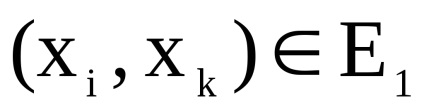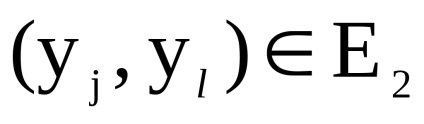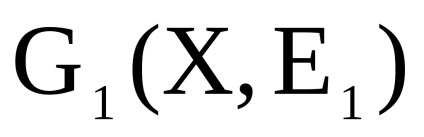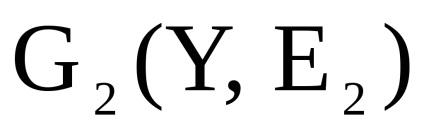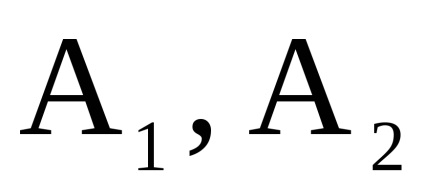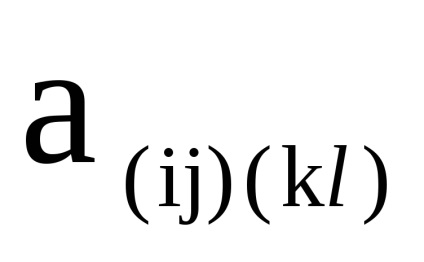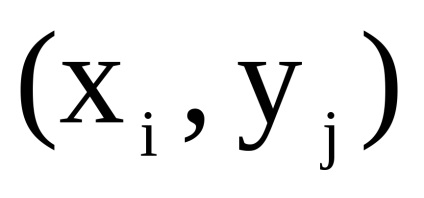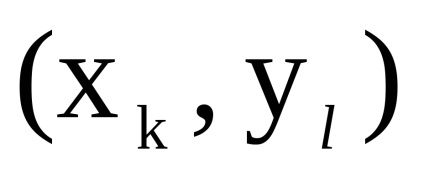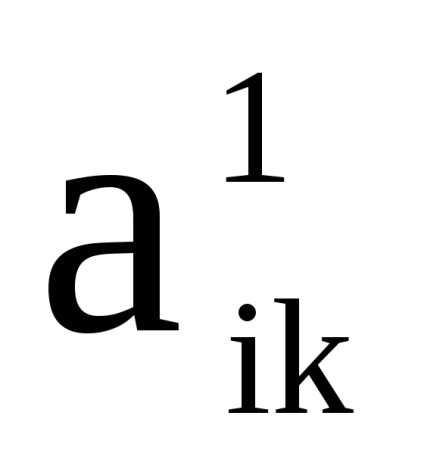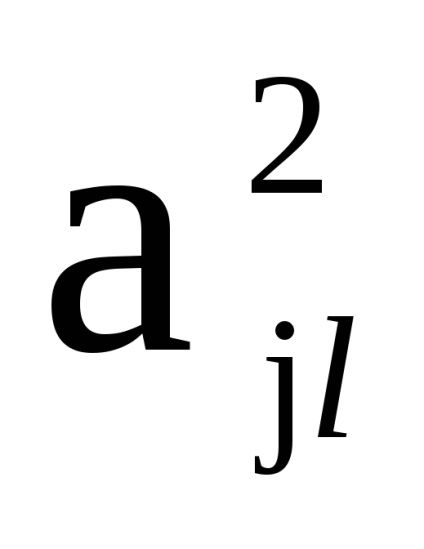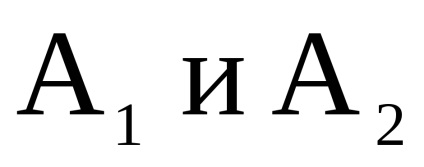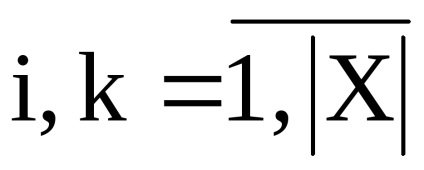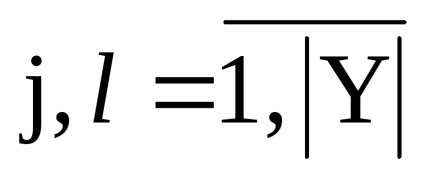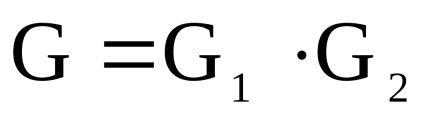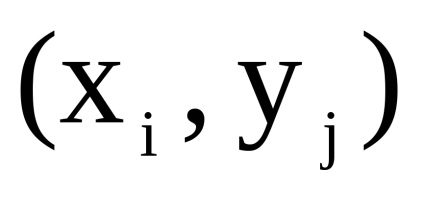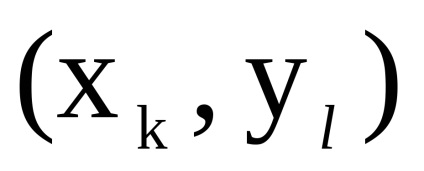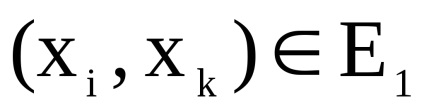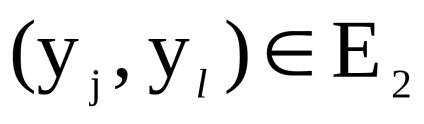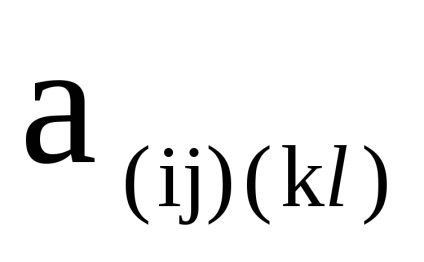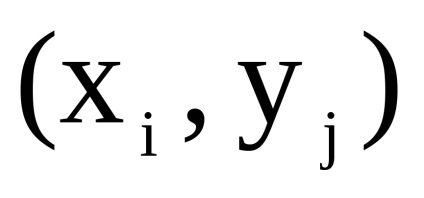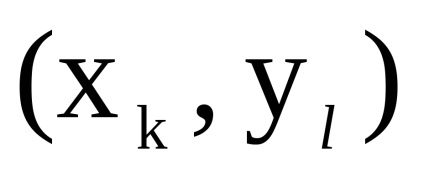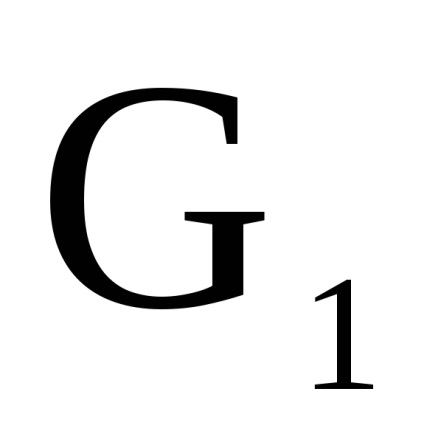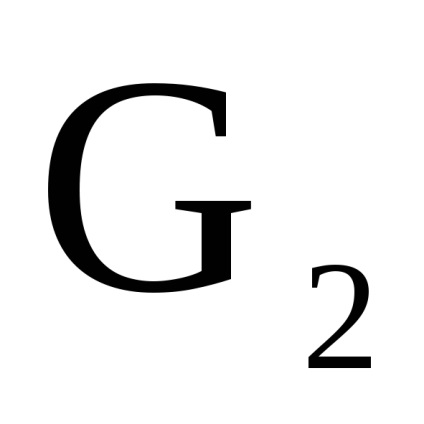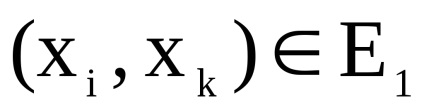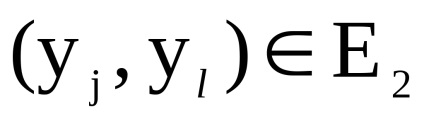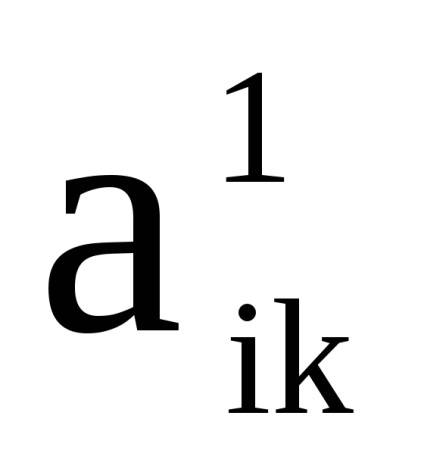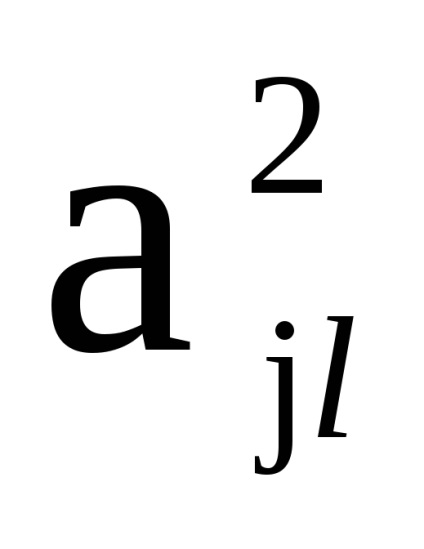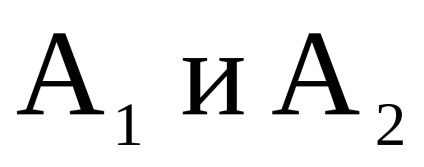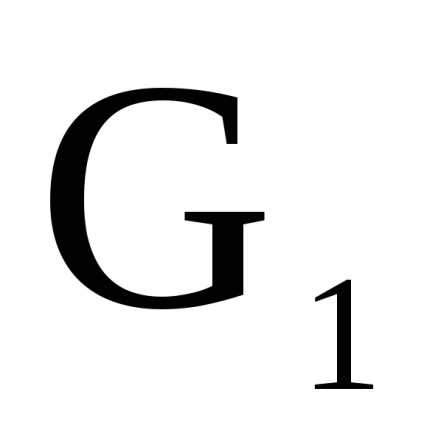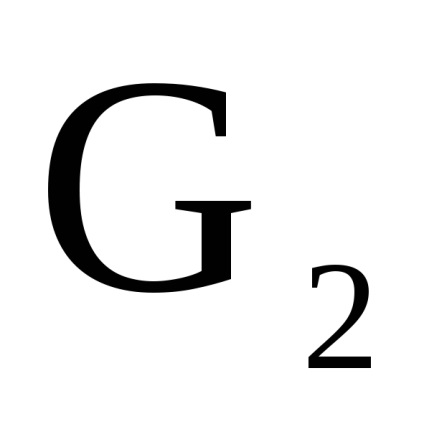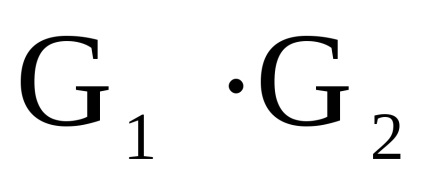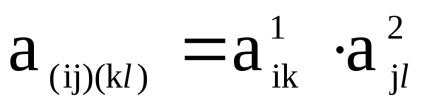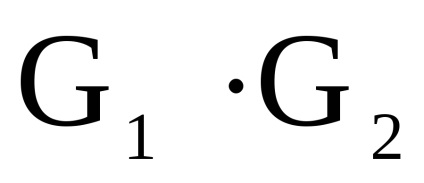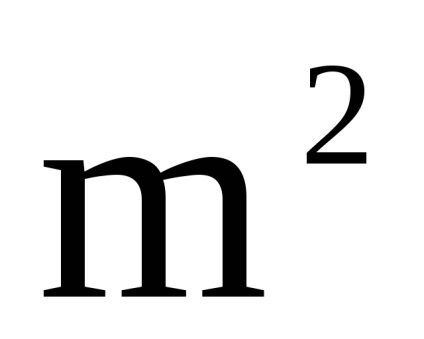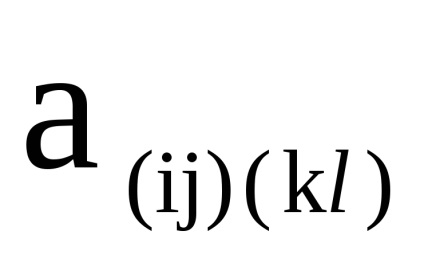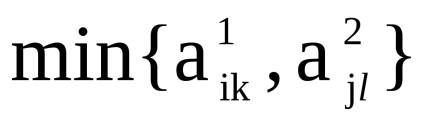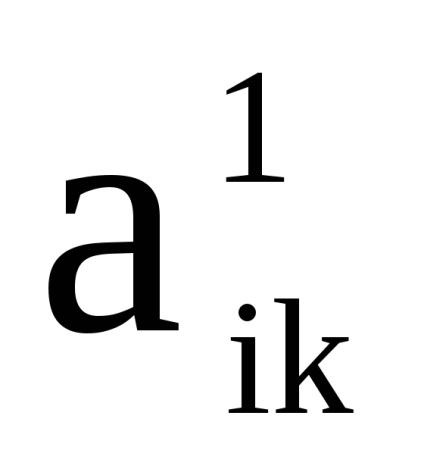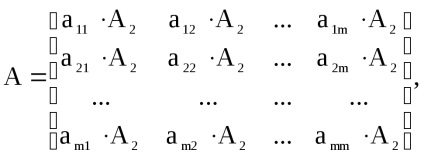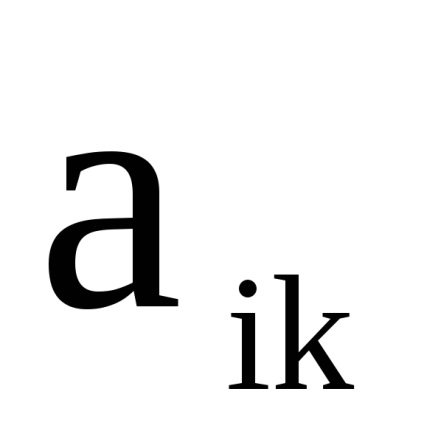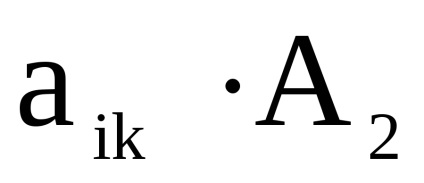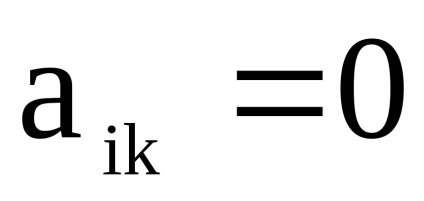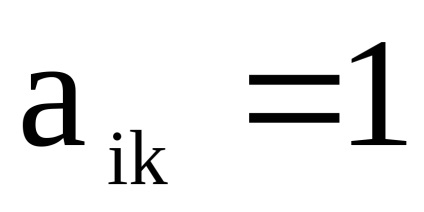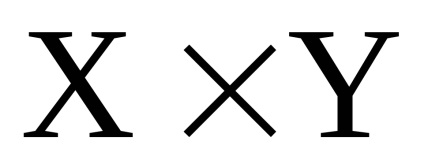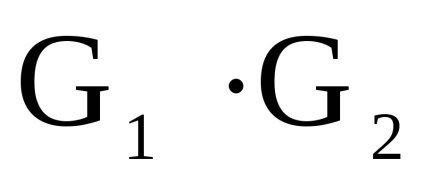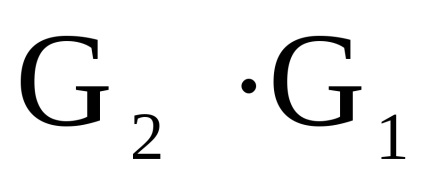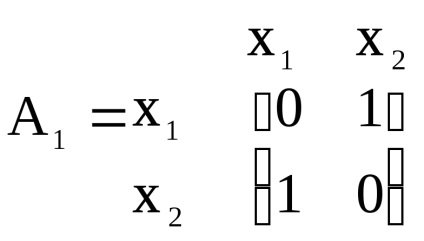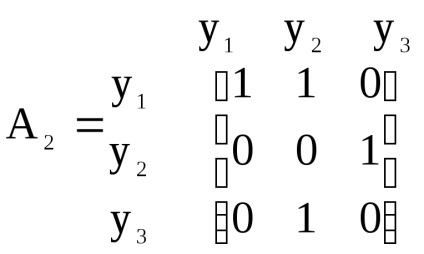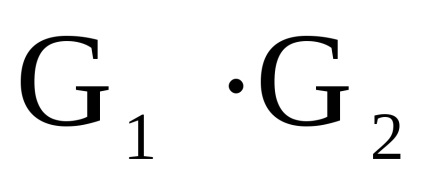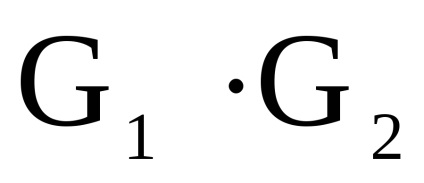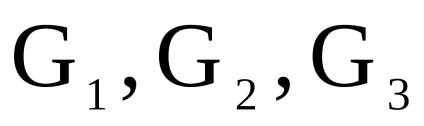Пряме твір графів 1

нехай

і - два одночасно орієнтованих або неорієнтованих графа з непересічними множинами вершін.Прямим творомграфів називається граф з безліччю вершин, в якому дуга (ребро) з вершини в вершину існує тоді і тільки тоді, коли існують дуги (ребра) і одночасно.

Розглянемо виконання операції прямого твори графів в матричної формі.

Теорема2.2.6. нехай

і - два одночасно орієнтованих або неорієнтованих графа з непересічними множинами вершин, - матриці суміжності їх вершин відповідно. Тоді матрицею суміжності вершин графа є матриця розмірності, в якій елемент , що рахує кількість дуг (ребер), що з'єднують вершину з , обчислюється таким чином:

,

де

і - елементи матриць відповідно, , .

Розмірність матріциAравна, а. За визначенням, в графі існує дуга (ребро), що йде з вершини в вершину , тоді і тільки тоді, коли одночасно існують дуги (ребра) і . Елемент матриці суміжності А графаG визначає кількість дуг (ребер) з вершини в вершину . Знаходження кількості дуг (ребер) графів і , для яких одночасно і , відповідає операції взяття мінімуму елементів і матриць відповідно.

Слідство. якщо графи

і не мають кратних дуг (ребер) і петля в неорієнтованому графі не рахується подвійний, то при обчисленні елементів матриці суміжності вершин графа операція взяття мінімального елемента відповідає обчисленню звичайного або логічного твори:

.

Зауваження. Для спрощення і прискорення процесу обчислення елементів матриці суміжності вершінAграфа

скористаємося наступним спостереженням. Без обмеження спільності, будемо вважати, що. Впорядкуємо стовпці і рядки матріциAследующім чином: Тоді матріцуAможно розбити на блоків, що відповідають елементам матриці А1. розмірністю . Елемент кожного блоку має фіксірованниеiіkі буде обчислюватися як , причому - фіксований елемент матриці А1. Якщо елементи матриць А1 і А2 приймають тільки значення 0 і 1, то - пряме (тензорне) твір матриць:

де

скалярно множиться на матрицю А2. дорівнює 0, якщо , і так само А2. якщо .

Прімер2.2.6. Рятувальна операція прямого твори графів зображено на рис. 2.2.12.

Очевидно, що відповідність між елементами множин

і визначає ізоморфізм графів і , що справедливо і в загальному випадку.

Складемо матриці суміжності вершин вихідних графів і.

, .

Згідно зі слідством з теореми 2.2.6 і зауваженням, матриця суміжності вершин графа

має вигляд:

Неважко переконатися в тому, що матриця суміжності вершин А відповідає графу

, зображеному на рис. 2.2.12.

Операція прямого твори графів має такі властивості, які випливають з визначення, а також властивостей декартова твори множин і справедливі для будь-яких одночасно орієнтованих або неорієнтовані графів

з непересічними множинами вершин:

Операцію прямого твори можна поширити по індукції на будь-яке кінцеве безліч орієнтованих або неорієнтовані графів з попарно що не перетинаються множинами вершин:

.

Схожі статті

• Пряме твір графів