Про початки геометрії (м Лобачевського).
У деяких бібліографіях описаний і 3-й складаний лист геометричних діаграм. Але при цьому в самому тексті знаменитої праці Лобачевського описані тільки ті 17 фігур поміщених на 2-х складних таблицях. У п / к палітурці епохи з потертим тисненням на корінці. Видавничі обкладинки до частини XXV збережені. Формат: 21х13 см. Рідкість!





4. Harrison D. Horblit. One hundred books famous in science. New York, 1964, №69а.
5. M. Kline. Mathematical thought from Ancient to Modern Times. New York, 1972, p.p. 873-81.
6. Біографічний словник діячів природознавства і техніки. Москва, 1959. Т. 1, стор. 524-527.
7. Dictionary of scientific biography (famous DSB), vol. VIII, New York, 1973, p.p. 428-434.
8. Болховітінов В. Буянов А. Захарченко В. Остроумов Г. Розповіді про російській першості. Під загальною редакцією В. Орлова. Москва, изд. «Молода Гвардія», друкарня Червоний прапор, 1950, стор. 47-51.
9. Люди російської науки. Нариси про видатних діячів природознавства і техніки. Т.1, Москва-Ленинград, ОГИЗ, 1948, стор. 90-98.
«Неминуща слава Лобачевського в тому, що він вирішив нам задачу, яка залишалася невирішеною дві тисячі років». С. Лі.
- За гріхи наші. - бурмотів колега Нікольський і боязко зиркав на Миколу Івановича. У вигляді Лобачевського йому зараз вчувалося щось сатанинське. Ось Микола Іванович зупинився біля дошки, якась чужа, нездешняя посмішка пробрела по його губах. Звів гострі вигнуті брови, насунув шапку темно-русявого волосся майже на очі, нахилив голову. Варто, затуливши спиною креслення, і, оглядаючи всіх похмуро-задумливим поглядом, каже:
-. Головний висновок, до якого прийшов я з припущенням залежності ліній від кутів, допускає існування геометрії більш у великому сенсі, ніж як її представив нам перший Заклад. У цьому розлогому вигляді дав я науці назву уявної Геометрії, де як окремий випадок входить вживана геометрія з тим обмеженням в загальному положенні, якого вимагають вимірювання справді. У чому ж суть, таємний зміст відкритої Лобачевским неевклідової геометрії? Чому великий геометр назвав її уявної? Чому евклідова геометрія є приватним - вірніше, граничним - випадком геометрії Лобачевського? Чи реальна геометрія Лобачевського в сенсі відповідності фізичного простору, чи існує поверхню, на якій справедлива нова геометрія, або ж вона даремний плід фантазії, безпідставний вимисел, гра уяви, формальний доказ незалежності п'ятого постулату від інших евклідова аксіом? Яка з двох геометрій з більшою точністю описує реальний світ? Крок за кроком ми простежили, як Лобачевський підходив до відкриття нової геометрії, простежили в тій мірі, в якій можливо розповісти про потаємної, найтоншої роботи геніального розуму, де з хаосу швидкоплинних спостережень на основі досвіду і інтуїції народжується небувала істина, поступово викристалізовується у вигляді чіткої формули. Перше значне відкриття Лобачевського складалося в доказі незалежності п'ятого постулату геометрії Евкліда від інших положень цієї геометрії. Другим відкриттям була вже сама логічно несуперечлива система нової геометрії. На свою геометрію він дивився саме як на теорію, а не як на гіпотезу. Прийшовши до логічного висновку, що в світовому просторі, а можливо і в. мікрокосмі, сума кутів трикутника повинна бути менше двох прямих, Лобачевський сміливо висунув свою вихідну аксіому, свій постулат і побудував незвичну геометрію, так само, як і евклідова, позбавлену внутрішніх суперечностей. Уявної назвав не тому, що вважав її формальним побудовою, а тому, що вона поки залишалася доступною лише уяві, а не досвіду. Його не покидала думка знову повернутися до вимірювання космічних трикутників і встановити істину. Нічого не змінюючи в «абсолютної» геометрії, він лише замінив п'ятий постулат Антіпостулат, антіевклідовой аксіомою: через зазначену точку можна провести безліч прямих, що не перетинають дану. На кресленні це виглядає так:
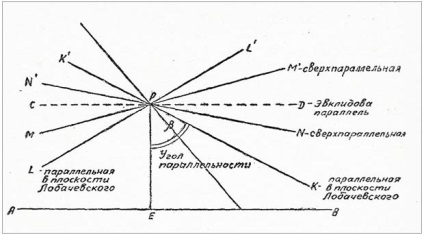
Лобачевський змінив саме розуміння паралельних ліній. У Евкліда непересічні і паралельні - одне і те ж, у Лобачевського: з усіх, що не перетинають дану пряму АВ (див. Креслення), лише дві прямі називаються паралельними - це К1РК. і LРL1. Всі інші, що знаходяться в пучку між паралельними, такими не вважаються (в сучасній літературі їх називають надпаралельні). Тому постулат уточнюється: якщо дана пряма АВ і не лежить на ній точка Р, то через точку Р в площині АВР можна провести дві прямі, паралельні даній прямій АВ. Паралельними Лобачевський, отже, називає такі, які відокремлюють непересічних від перетинають дану пряму АВ. Відстань між прямою АВ і кожної з паралельних не залишається постійним - зменшується в сторону паралелізму і збільшується в протилежну сторону. Паралельні прямі можуть близько підійти один до одного, але вони не можуть перетнутися. Площина, в якій існують такі паралельні, прийнято називати площиною Лобачевського. Ця площина зовсім не «плоска» в евклідовому смисле.В евклідовой площині кут паралельності незмінний і завжди дорівнює 90 °; в геометрії Лобачевського він може приймати всі значення - від 0 до 90 °. Отже, евклідова геометрія є приватний (граничний) випадок геометрії Лобачевського, в якій кут паралельності змінний. Геометрично величина кута паралельності залежить від довжини X перпендикуляра РЕ; тобто якщо перпендикуляр зменшується, кут паралельності збільшується, поступово наближаючись до 90 °. Дуже умовно на кресленні це можна було б уявити так:
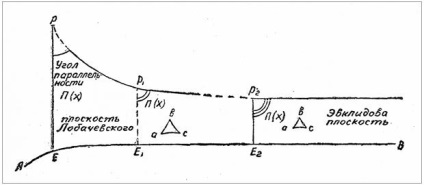
Іншими словами: коли точка Р прагне до збігу з точкою Е, тобто коли X прагне до нуля тоді кут паралельності прагне до 90 °. Таким чином, в новій геометрії існує взаємозалежність кута і відрізка. Коли кут паралельності прямої, тобто дорівнює 90 °, взаємозалежність зникає. У евклідовой геометрії її немає. У неевклідової вона представляє найбільш значний момент. З цієї взаємозалежності виводиться основна формула всієї геометрії Лобачевського. У формулу Лобачевський вводить так звану лінійну константу. У сучасній науці під лінійної константою розуміють радіус кривизни простору Лобачевського; величина константи залежить від конкретних фізичних умов в даній частині світового простору. Виключно велика величина константи свідчить про те, що наш простір має величезний радіусом кривизни і, отже, досить малої, близькою до нуля, кривизною, тобто простір в нашій частині всесвіту має плоский, Евклід характер. Але якщо допустити, що лінійна константа може мати різні значення, то кожному з подібних значень буде відповідати своя, особлива геометрія. Отже, може мати місце безмежну кількість різних геометрій. Для Канта простір - незмінна сутність; для Лобачевського - воно форма існування матерії. Простір здатне змінюватися разом з матерією. Так, так, Лобачевський створив дивну геометрію. Тут немає подібних фігур; сума кутів трикутника завжди менше двох прямих, причому в міру збільшення трикутника вона прагне до нуля. Спробуйте уявити собі трикутник, сума кутів якого дорівнює нічому! А трикутників як завгодно великої площі в цій дивній геометрії взагалі не може бути. Тут існує пряма залежність між кутами і довжиною сторін трикутника, чого немає в евклідовой. Тут відсутні прямокутники. Іншими є і співвідношення для окружності. Площина і простір Лобачевського мають постійну негативну кривизну і т.д. «Ньютон - найбільший геній і найщасливіший з усіх, тому що система світу тільки одна і відкрити її можна було лише одного разу», - сказав Лагранж. Відмовившись від ньютоновой концепції простору і часу, Лобачевський створив новий світ - грандіозний «світ Лобачевського», в якому звичний нам Евкліда світ є лише граничним випадком, нескінченно малої областю простору, де ми повзаємо, подібно мурашкам. Ця нескінченно мала частина простору вміщує всі наші радості, надії, трагедії, наше минуле і сьогодення, весь сенс нашого існування.
-. Не можна не захоплюватися думкою Лапласа, - звучав густий голос Лобачевського, - що видимі нами зірки належать до одного тільки зборам небесних світил, подібно до тих, які вбачаємо як слабо мерехтливі плями в сузір'ях Оріона, Андромеди, Козерога і інших. Отже, не кажучи про те, що в уяві простір може бути продовжено необмежено, сама природа вказує нам такі відстані, в порівнянні з якими зникають за малістю навіть і відстані нашій землі до нерухомих зірок. Волосся ворушилися на голові Нікольського. Він крадькома хрестився і все бурмотів:
- За гріхи наші, господи помилуй.
Справа в тому, що в Петербурзі проживав ще один математик Лобачевський, далекий родич Миколи Івановича. Цей петербурзький Лобачевський, Іван Васильович, був одержимий ідеєю про квадратуру кола і набридав Остроградскому. У столі у Остроградського лежала робота Івана Васильовича «Геометрична програма, яка містить ключ до квадратурі нерівних луночек (3: 4) (1: 4) і сегмента в складі полуразность оних знаходиться». Розгорнувши мемуари «Про початки геометрії» казанського Лобачевського, Остроградський жахнувся. Що за маячня. Цьому Лобачевському мало квадратури кола, тепер він зайнявся теорією паралельних! Винайшов нову геометрію - уявну. Важко мати справу з божевільними. Михайло Васильович написав розмашисто: «Сей Лобачевський непоганий математик, але якщо треба показати вухо, то він показує його ззаду, а не спереду». Фусс люб'язно пояснив академіку Остроградскому, що цей Лобачевський зовсім не той Лобачевський, а ректор Казанського університету.
- Тоді інша справа, - сказав Михайло Васильович і написав:
«Можна перевершити самого себе і прочитати погано средактірованний мемуари, якщо витрата часу спокутується пізнанням нових істин, але більш важко розшифровувати рукопис, яка їх не містить і яка важка не височиною ідей, а вигадливим оборотом пропозицій, недоліками в ході міркувань і нарочито застосовуваними дивацтвами. Ця остання риса властива рукописи пана Лобачевського. Нам здається, що мемуари пана Лобачевського про збіжність рядів не заслуговує схвалення Академії ».
- Тут тебе поминають.
- Так то краще! - сказав Мусін-Пушкін.
Список творів Лобачевського:
1. 1823. Геометрія. Видано в 1909 р Казанським Фізико-математичним Товариством. До «Геометрії» прикладені два докази постулатума Евкліда, які Лобачевський викладав в своїх лекціях 1815-17 р
6. 1834. Зниження ступеня в двучленном рівнянні, коли показник без одиниці ділиться на 8 ( «Вчені Записки», 1834 І, стор. 3-32).
7. 1834. Про зникання тригонометричних рядків ( «Вчені Записки», 1834 II, стор. 167-226).
9. 1835. Уявна геометрія ( «Вчені Записки», 1835, І, стор. 3-83, табл. З фіг. 1-8). Майже збігається з № 13. Передруковано в Повному зібранні творів, т. І, стор. 71-120.
10. 1835. Спосіб запевняють в зникання нескінченних рядків і наближатися до значення функцій від вельми великих чисел ( «Вчені Записки», тисячі вісімсот тридцять п'ять, II, стор. 211-342).
11. 1835-1838. Нові початку геометрії з повною теорією паралельних ( «Вчені Записки», 1835, III. Стор. 3-48. Введення і глава І, І таблиця, фіг. 1-20; тисячі вісімсот тридцять шість, II, стор. 3-98, глави IІ - V, 3 табл. фіг. 21-41, 42-60, 61-75; 1836, III, стор. 3-50, глави VI-VII, 2 табл. фіг. 76-91, 92-106; 1837 І . стор. 3-97, глави VIII-XI, 2 табл. фіг. 107-120, 121-134; 1 838, І, стор. 3-124, глава XII; 1 838, III, стор. 3-65, глава XIII ). Передруковано в Повному зібранні творів, т. І, стор. 219-486.
12. 1836. Застосування уявної геометрії до деяких інтегралів ( «Вчені Записки», 1836, І, стор. 3-166, 1 таблиця, фіг. 1-20). Передруковано в повному зібранні творів, т. І, стор. 121-218.
13. 1837. Géométrie imaginaire par М-r. N. Lobatschewsky, recteur de l'Université de Cazan. (Журнал Крелль. T. 17, тетр. 4, стор. 295-320, 1 табл. Фіг. 1-8. Берлін 1837; послано в 1834 або 1835 г.). Передруковано в Повному зібранні складений. т. II, стор. 581-613.
16. 1842. Sur la probabilité des résultats moyens, tirés des observations répétées. (Par Mr. Lobatschefsky, recteur de l'université de Cazan. Journal der reinen und angewandten Mathematik von Grelle. Bd. 24. Heft. 2, стор. 164-170). Переклад деяких сторінок з голови XII «Нових почав». Повне зібрання творів, стор. 428-438.
18. 1845. Докладний розбір міркування, представленого магістром А. Ф. Поповим під назвою: «Про інтегруванні диференціальних рівнянь гідродинаміки, приведених до лінійного вигляду», на ступінь доктора математики і астрономії. Додаток до докторської дисертації Попова. Казань, тисячі вісімсот сорок п'ять.
19. 1852. Значення деяких визначених інтегралів ( «Вчені Записки» 1852 г. т. IV, вип. I, стор. 1-26; вип. II, стор. 27-34). Ця робота з'явилася і на німецькій мові в видавався Г. А. Ерманом «Archiv für wissenschaftliche Kunde von Russland». Berlin 1855. Bd. 14, стор, 232-272, під заголовком: «Ueber den Werth einiger bestimmten Integrale. Nach dem Russischen von Herrn Lobatschefskji, Prof. emer. in Kasan ».
20. 1856. Pangéométrie ou précis de géométrie fondée sur une théorie générale et rigoureuse des parallèles, par N. Lobatscheffsky, professeur émérite de l'université de Kasan et membre honoraire de l'université de Moscou (Збірник наукових статей, написаних професором Імператорського Казанського університету, в пам'ять п'ятдесятирічного його існування, т. І. Казань. 1856 стор. 279-340. Передруковано в Повному зібранні творів, т. II, стор. 617-680).
21. 1855. Пангеометрия, заслуженого професора Н.І. Лобачевського ( «Вчені Записки», 1855, т. І, стор. 1-56; Казань, 1856 р Збігається з № 20. Передруковано в Повному зібранні творів, т. І, стор. 489-550).