ПРО РІШЕННЯ одновимірних НЕОДНОРІДНОГО хвильового рівняння У КІНЦЕВОМУ ВИГЛЯДІ
1 ФГБОУ ВПО «Уфимський державний нафтової технічний університет»
У даній роботі запропоновано спосіб інтегрування одновимірного неоднорідного хвильового рівняння, при якому спільне рішення містить чотири довільні функції. Ця ідея реалізована при отриманні формули (7). Наявність чотирьох довільних функцій надає широкі можливості при отриманні рішення, коли є які-небудь обмеження на шукану функцію. Про те, як можна розпорядитися цими функціями, показано на прикладі завдання з початковими і однорідними граничними умовами. Рішення, що містить кінцеве число членів, названо рішенням в кінцевому вигляді, на відміну від звичайного способу вирішення через нескінченний тригонометричний ряд. Зручність рішення в кінцевому вигляді проявляється в наближених розрахунках, в яких відпадає необхідність з'ясовувати, скільки членів тригонометричного ряду потрібно залишити, щоб досягти необхідної точності рішення.
рішення в кінцевому вигляді
1. Арамановіч І.Г. і Левін В.І. Рівняння математичної фізики. М. Наука, 1964. - 288 с.
2. Корн Г. Корн Т. Довідник з математики для науковців та інженерів. М. Наука, 1974. - 832 с.
3. Кошляков Н.С. Глінер Е.Б. Смирнов М.М. Рівняння в приватних похідних математичної фізики. М. Вища школа, 1970. - 712 с.
4. Прудников О.П. Брички Ю.А. Марічев О.І. Інтеграли і ряди. М. Наука, 1981. - 800 с.
5. Тихонов А.Н. Самарський А.А. Рівняння математичної фізики. М. Наука, 1966. - 724 с.
У статті розглядається диференціальне рівняння виду
Воно описує малі поперечні, поздовжні і крутильні коливання однорідного стержня. Звичайний спосіб вирішення такого рівняння полягає у знаходженні рішення в вигляді нескінченного тригонометричного ряду [1, 3, 5]. У даній роботі пропонується метод, що дає рішення в кінцевому вигляді.
1. Спочатку знайдемо спільне рішення рівняння (1). Перейдемо до нових змінних
Функція перейде в функцію
,
і рівняння (1) призведе до виду
Інтегрування рівняння (3) по змінній дасть
де - довільні функції. Проинтегрировав (5) по отримаємо
де - довільні функції.
Нехай - первісна функція від В цьому випадку
і (6) запишеться у вигляді
Замінивши за формулами (2), отримаємо загальне рішення вихідного рівняння
2. Як приклад застосування даного методу вирішимо рівняння (1), в якому покладемо взявши область зміни змінних
і однорідні граничні умови
Виконавши в (1) заміну
отримаємо рівняння виду (3):
спільне рішення якого дається рівністю (7). Уявімо це рівність у вигляді
З цих рівностей випливають відповідності:
Тому з (8) виходить наступна область зміни змінних (малюнок):
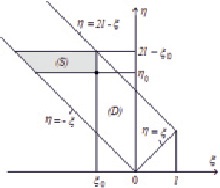
Необмежена смуга (D) - область зміни змінних ξ, μ (S) - область, прийнята в якості області інтегрування в подвійному інтегралі
Усередині візьмемо довільну точку і побудуємо ділянку як показано на малюнку. Ця ділянка задається системою нерівностей
Відповідно до (14) значення функції в точці дорівнює
Область інтегрування визначається системою нерівностей
В силу довільності функцій виберемо їх такими, щоб система нерівностей (17) збіглася з (16): Вираз (14) набуде вигляду
Залучимо умови (9) - (10), щоб знайти решту функції і
Запишемо умови (9) - (10) в змінних використовуючи відповідності (15):
Науковий журнал | ISSN 1812-7339 | ПІ №77-63397
Служба технічної підтримки - [email protected]
Відповідальний секретар журналу Бізенкова М.Н. - [email protected]
Матеріали журналу доступні на умовах ліцензії Creative Commons «Attribution» ( «Атрибуція») 4.0 Всесвітня.