Вивчення першого розділу курсу нарисної геометрії засновано на использова-
ванні отриманих студентами знань в школі з геометрії. Тому правила побудови проекцій точок, прямих ліній і площин вивчається в курсі на прикладах побудови проекцій простих тіл - правильних багатогранників.
Багатогранник - частина простору, обмежена сукупністю кінцевого числа плоских багатокутників, з'єднаних таким чином, що кожна сторона будь-якого багато-
кутника є стороною рівно одного іншого багатокутника, званого смеж-
вим. Причому, навколо кожної вершини існує рівно один цикл багатокутників. Ці багатокутники називаються гранями, лінії перетину граней - ребрами, точки пересе-
чення ребер - вершинами многогранника.
Розглянемо побудову зображень багатогранників. В основу отримання изобра-
жений на кресленні покладено метод прямокутного проектування на дві взаімно-
перпендикулярні площини проекцій. При цьому багатогранник розташовують відносна
але площин проекцій так, щоб максимальна кількість граней проектувалося на фрон-
тальне площину π 2 без спотворення. Підстава зазвичай розташовують паралельно гори-
зонтальним площині проекцій.
Домашнє завдання, яке виконує студентами, має на меті навчити будувати проек-
ції точок, прямих ліній і площин, і визначати їх взаємну належність на зображеннях призми і піраміди.
Домашнє завдання складається з наступних розділів:
1. Побудова проекцій призми і перетин її проецирующей площиною.
2. Побудова проекцій піраміди і перетин її проецирующей площиною.
Послідовність виконання домашнього завдання:
1. Побудова проекцій призми.
2. Перетин призми проецирующей площиною.
3. Побудова проекцій піраміди.
4. Перетин піраміди проецирующей площиною.
5. Побудова розрізів.
Т.Л. Бєлобородова, Є.Ю. Кичигина. Проекції багатогранників.
Побудова проекцій призми
Наступні ознаки дозволяють стверджувати, що зображення є ізображе-
ням саме призми (або, зокрема, паралелепіпеда):
- наявність тільки прямолінійних відрізків, причому вони служать проекціями або ре-
бер, або граней; - наявність паралелограмів або прямокутників як проекцій бічних граней;
-наявність будь-якого багатокутника як проекції підстави.
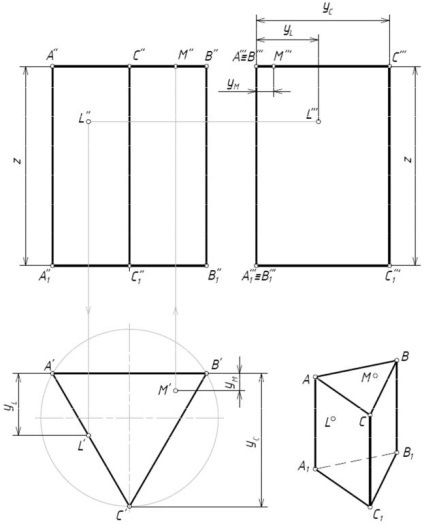
Побудуємо зображення правильної трикутної призми (Рис.1). підставою приз
ми служить правильний трикутник ABC. паралельний горизонтальній площині проек-
ций. Тому на горизонтальну площину він проектується в натуральну величину - проекція A'B'C'. Так як бічні грані призми є горизонтально проектується площинами, то кожна сторона трикутника A'B'C' є горизонтальною проекцією межі. Ребра призми є горизонтально проектується прямими, тому кожна вершина трикутника A'B'C' є горизонтальною проекцією ребра призми; соответ-
ного ребра AA 1. BB 1, CC 1 проектуються в точки A', B', C'.
Побудуємо фронтальну проекцію призму (вид спереду). Фронтальною проекцією є прямокутник A''A 1''B 1''B''. Сторони A''A 1'' і B 1''B'' є проекціями ребер AA 1. BB 1. а боку A''B'' і A 1''B 1'' - проекціями верхнього і нижнього підстав призми. Проекція ребра CC 1 - C''C 1'' розташована всередині прямокутника і поєднується з віссю симетрії. Прямокутник A''A 1''B 1''B'' є проекцією межі AA 1 B 1 B. парал-
інтер- фронтальній площині проекцій і проектується на цю площину без спотворення.
Дві інші бічні грані AA 1 С 1 С і BB 1 C 1 C проектуються з спотворенням на фронтальну площину π 2.
Профільну проекцію призми будуємо, використовуючи координати у і z (Рис.1). про-
профільними проекція призми - прямокутник A''A 1''С 1''С'' з вершинами A''' ≡ B''', A 1''' ≡ B 1''',
З 1. С'''. Сторона прямокутника A'''A 1''' (B'''B 1''') є проекцією бічній грані
AA 1 B 1 B і ребер AA 1 і ВВ 1. належать цій межі. Грань AA 1 B 1 B паралельна фрон-
ментальною площині π 2 і перпендикулярна горизонтальній площині π 1 і профільної плос-
кістки π 3. Сторона С'''С 1''' - проекція ребра СС 1. Прямокутник A'''A 1'''С 1'''С''' є і проекцією межі AA 1 С 1 С. а також межі CC 1 B 1 B. яка закрита гранню AA 1 С 1 С. Так як обидві грані не паралельні профільній площині проекцій, то вони проектуються з іска-
жениями. Всі бічні ребра призми на фронтальній і профільній площинах проекцій
Т.Л. Бєлобородова, Є.Ю. Кичигина. Проекції багатогранників.
проектуються без спотворення, так як вони є горизонтально-проектується пря-
мимі, отже, паралельні фронтальній і профільній площинах проекцій.
Т.Л. Бєлобородова, Є.Ю. Кичигина. Проекції багатогранників.
Знайдемо відсутні проекції точок - L, M.
Точка L задана фронтальною проекцією L'' і належить межі AA 1 С 1 С.
Для побудови горизонтальної проекції точки L через точку L'' проведена лінія верти-
кальной зв'язку до перетину з прямою A'C'. в яку проектується грань AA 1 С 1 С. На ли-
ванні горизонтального зв'язку за допомогою координати у L знаходимо профільну проекцію точ-
ки L (L'''). Точка M задана горизонтальною проекцією M'і належить верхньому основа-
нию призми. Фронтальна проекція точки M знайдена на перетині вертикальної лінії зв'язку, проведеної через M'. з відрізком прямої A''B'' - проекцією верхнього підстави призми. Профільна проекція точки M (M''') отримана за допомогою координати у M.
Т.Л. Бєлобородова, Є.Ю. Кичигина. Проекції багатогранників.
Перетин призми проецирующей площиною
Розглянемо перетин правильної шестикутної призми проектується плос-
Площина γ 1 нахилена до осі призми під кутом α 1 і перпендикулярна фронтальної
площині. Ця площина перетинає ребра призми в точках A. K і K 1. а дві грані призми за прямими AK (A'K', А''К''), АК 1 (А'К' 1. А''К 1'')
З огляду на наявність площині γ 2. паралельної π 1. отримаємо:
- на фронтальній площині проекцій - прямі А''К'' (А''К 1''), збігаються з фронтальною проекцією площини - γ 1'';
- на горизонтальній площині - трикутник А'К'К 1 '. вершини якого збігаються
з вершинами шестикутника - проекцією нижньої основи призми;
- на профільній площині - трикутник А'''К'''К 1'''. вершини якого побудова
ни за допомогою горизонтальних ліній зв'язку та координат У.
При перетині призми горизонтальною площиною γ 2 отримаємо:
- на фронтальній площині проекцій - прямі К''М'' (К 1''М 1'') збігаються з фронтальною проекцією площини - γ 2'';
- на горизонтальній площині проекцій - чотирикутник К'М'М 1 'К 1'. вершини якого К'і К 1 'збігаються з вершинами шестикутника - проекцій нижньої основи призми, а сторона М'М 1' є горизонтальною проекцією прямої перетину фрон-
тально-проектують площин γ 2 і γ 3 (фронтальна проекція лінії ММ 1 - точ-
- на профільній площині проекцій - прямі К''К 1''' (M'''M 1''') побудовані з по-
міццю горизонтальних ліній зв'язку.
Площина γ 3 нахилена до осі призми під кутом α 2 і перпендикулярна фронтальної площини.
Площина γ 3 перетинає передню і задню грані за прямими МN і М 1 N 1.
В результаті перетину отримаємо:
- на фронтальній площині проекцій - проекції прямих M''N'' (M 1''N 1'') збігатися
дуть з проекцією площини γ 3'';
- на горизонтальній площині проекцій - чотирикутник М'N'N 1'M 1 ';
Т.Л. Бєлобородова, Є.Ю. Кичигина. Проекції багатогранників.
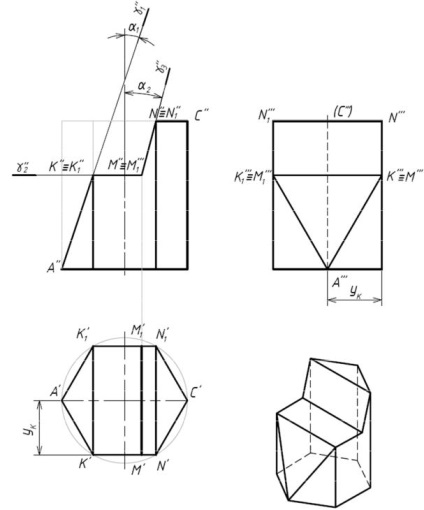
- на профільній площині проекцій - чотирикутник M'''N'''N 1'''M 1'''.
Т.Л. Бєлобородова, Є.Ю. Кичигина. Проекції багатогранників.
Побудова проекцій піраміди
Наступні ознаки дозволяють стверджувати, що зображена піраміда:
-наявність тільки прямолінійних відрізків, які служать проекціями ребер або граней,
- наявність трикутників як проекцій бічних граней; -наявність будь-якого багатокутника як проекції підстави;
-наявність вершини піраміди як точки перетину бокових ребер.
Побудуємо проекції правильної трикутної піраміди (Рис.3). піраміда називает-
ся правильної, якщо підставою піраміди є правильний багатокутник, а бічні грані - рівні трикутник і підставою висоти правильної піраміди є центр описаної (або вписаною) близько багатокутника кола.
Підстава піраміди сумісний з горизонтальною площиною проекцій, на цю площину воно проектується в натуральну величину. При цьому висота піраміди на гори-
зонтальним площину проектується в точку. Щоб побудувати горизонтальну проекцію піраміди, на горизонтальній площині з точки S'. як з центру, проведемо окружність і впишемо в неї рівносторонній трикутник (Рис. 3). Вершини його з'єднаємо прямими з точкою S '. Отримана фігура є горизонтальною проекцією піраміди: Δ А'В'С' -
горизонтальна проекція підстави піраміди; S'- горизонтальна проекція верші-
ни, а прямі S'A', S'B' і S'C' - горизонтальні проекції ребер піраміди. Так як основа піраміди перпендикулярно фронтальній площині, то фронтальною проекцією підстави є пряма. Добудуємо фронтальну проекцію. Через точку S'проведемо вертикальну лінію зв'язку і відкладемо на ній від фронтальної проекції підстави А'В'С' висоту пірамі-
ди. Отримаємо точку S'' - фронтальну проекцію вершини піраміди. З'єднаємо її з точка
ми B'', A'', C'' Отримаємо фронтальну проекцію піраміди, де S''B''A'' і S''A''C'' -
фронтальні проекції бічних граней SBA і SAC. а S''B''C'' - фронтальна проекція зад
ній межі SBC. Профільну проекцію будуємо, використовуючи фронтальну і горизонтальну проекції.
Відзначимо, що площині граней SAB і SAC загального положення, а площину
На межі SAB задана горизонтальна проекція точки K. Потрібно побудувати фрон-
тальне і профільну проекції цієї точки. Для цього треба побудувати проекції прямої,
що належить площині загального положення SAB і проходить через точку K. Через го-
-різонтального проекцію K'проводимо пряму 1'2' паралельно стороні підстави AB. по-
Т.Л. Бєлобородова, Є.Ю. Кичигина. Проекції багатогранників.