1.3. Поверхня в проекціях з числовими відмітками
Поверхня в проекціях з числовими відмітками зазвичай задаються своїми горизонталями. Горизонталі поверхні можна уявити як лінії перетину цих поверхонь горизонтальними площинами, проведеними з постійним кроком. Побудова таких горизонталей є завданням градуювання поверхні. Лінія ската стосовно до поверхонь зазвичай розглядається для конкретної точки і проводиться перпендикулярно горизонталях, що проходить через неї.
Завдання градуювання є часто зустрічається завданням, розв'язуваної стосовно до поверхонь в проекціях з числовими відмітками.
Розглянемо рішення цієї задачі для деяких поверхонь.
а. конічна поверхня
Конічна поверхня може бути представлена як прямим конусом з вертикальною віссю, так і похилим конусом, розглянемо спочатку прямий конус (рис. 18, а). Перетину конічної поверхні горизонтальними площинами дадуть ряд кіл. У разі прямого конуса, проектуючи їх на горизонтальну площину, отримуємо ряд концентричних кіл (рис. 18, б). Лінію найбільшого ската для прямого конуса можна отримати, проградуювати утворить конуса. Для виконання цієї операції необхідно знати позначку будь-яких двох точок на утворює або позначку однієї точки і ухил.
Дещо складніше справа йде в тому випадку, якщо конус похилий. Центри кіл, одержуваних при його розтині паралельними площинами, що не лежать на одній вертикальній осі і, отже, при проектуванні їх на горизонтальну площину НЕ
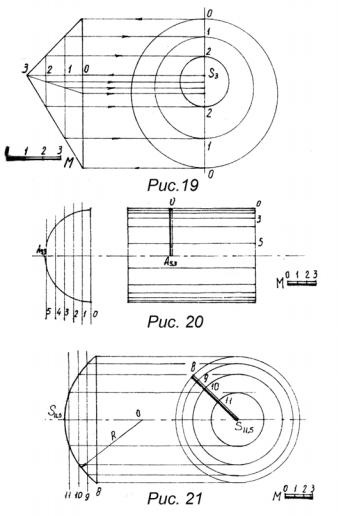
дадуть проекцій у вигляді концентричних кіл. Для градуювання похилого конуса (рис. 19) градуируют його найдовшу і найкоротшу утворить. Знаходять на утворюють точки з однаковими відмітками, вони відзначають діаметр окружності є горизонталлю. Для відшукання центру цього кола можна скористатися розподілом відрізка (діаметра) на дві рівні частини або, як показано на малюнку 19, провести вісь вертикальної проекції конуса, якій ці центри кіл належать.
б. циліндрична поверхня
Якщо утворюють циліндра вертикальні, то горизонтальна проекція циліндра являє собою коло, т. Е. Є виродження. В цьому випадку в проекціях з числовими відмітками вказують на вироджених проекції позначку верху циліндра. Особливого інтересу цей випадок не становить. Якщо вісь циліндра горизонтальна, то завдання градуювання поверхні зводиться до відшукання утворюють, позначки яких виражені цілими числами. Для цього будуємо вертикальну проекцію циліндра або тієї його частини, яку необхідно проградуювати (рис. 20). Проградуювати її по висоті, проведемо вертикальні проекції горизонтальних площин. Відзначимо точки їх перетину з вертикальною проекцією циліндра і перенесемо на проекцію з числовими відмітками проекції шуканих утворюють. Лінія ската для будь-якої точки такої поверхні є дугу окружності.
в. сферична поверхня
Градуювання сферичної поверхні проводиться за тим же принципом, що і градуювання поверхні циліндричної (рис. 21). Будується вертикальна проекція сфери, градуюється її вертикальна вісь, знаходяться точки перетину вертикальних проекцій горизонтальних площин з вертикальною проекцією сфери. Потім на фронтальній проекції сфери відзначають радіуси кіл, які відсікають горизонтальні площини на поверхні сфери. Цими радіусами проводять шукані кола є горизонталями сфери на проекції з числовими відмітками. Лінія ската для будь-якої точки сферичної поверхні являє собою дугу окружності.
м Поверхность рівного ухилу
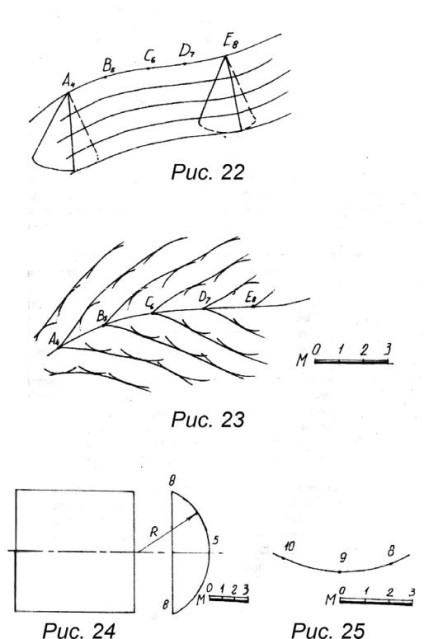
Якщо прямий круговий конус за вершину переміщати по довільній кривій (рис. 22), то отримана при цьому переміщенні поверхню називається поверхнею рівного ухилу. Конус є визначником цієї поверхні, а крива служить направляє. Для будь-якої точки такої поверхні лінія ската має однаковий нахил до горизонтальної площини. При градуювання поверхні однакового ската потрібно мати на увазі, що ухил поверхні в будь-який її точці однаковий і відстань між суміжними горизонталями одно інтервалу лінії ската. Для градуювання розміщуємо конуси в точках заданої направляє кривої і градуіруем їх поверхні. На практиці (рис. 23) це виглядає як проведення з точок кривої концентричних кіл, радіуси яких відрізняються на величину інтервалу, а висотні позначки на одиницю. Провівши криві лінії, дотичні з цими горизонталями конічних поверхонь, що мають одну і ту ж позначку, отримаємо горизонталі поверхні рівного ухилу.
1. Чим зазвичай задаються поверхні в проекціях з числовими відмітками?
2. Що являють собою горизонталі поверхні?
3. Що означає проградуювати поверхню?
4. Що являють собою горизонталі конуса?
5. Чим відрізняється градуювання прямого і похилого конусів?
6. Що спільного між градуюванням сферичної і циліндричної поверхні?
7. Що являють собою горизонталі циліндричної поверхні?
8. Що представляють собою горизонталі сферичної поверхні?
9. Що являє собою поверхню рівного ухилу?
10. Що є визначником поверхні рівного ухилу?
11. Що є направляючої поверхні рівного ухилу?
12. Як градуируют поверхню рівного ухилу?
1. проградуювати циліндричну поверхню (рис. 24).
2. проградуювати поверхню рівного ухилу (рис. 25).
1.3. топографічна поверхня
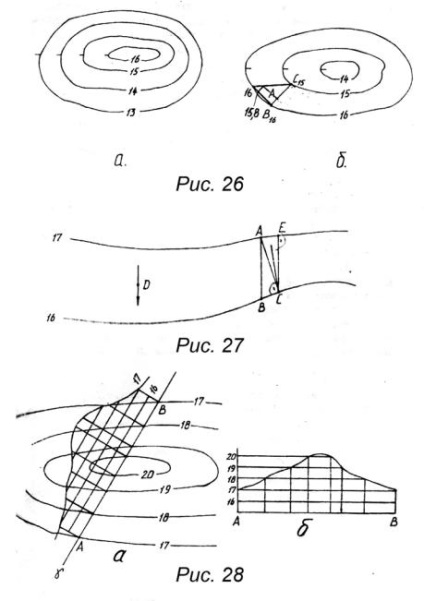
Земна (топографічна) поверхню представляється горизонтальною проекцією каркасної моделі, що утворюється при розтині земної поверхні горизонтальними площинами. За зростанням горизонталей можна судити про вид зображуваної поверхні. Так, на малюнку 26, а зображено підвищення місцевості (пагорб), а на малюнку 26, б її зниження. На додаток до висотних позначок на горизонталях зазвичай проставляються бергштрихи, що показують напрямок зниження місцевості. Важливим припущенням в проекціях з числовими відмітками є припущення про лінійний характер зміни місцевості між її горизонталями. Це припущення дозволяє вирішувати наступні завдання:
1. Знаходити позначки проміжних точок місцевості (рис. 26, б).
Наприклад, для визначення позначки точки A проведемо через неї відрізок довільного напрямку. Початок (т. B) і кінець (т. C) відрізка знаходяться на сусідніх з точкою A горизонталях. Провівши операцію, відповідну градуировке відрізка (див. П. 1.1), визначимо позначку точки A (-15,8).
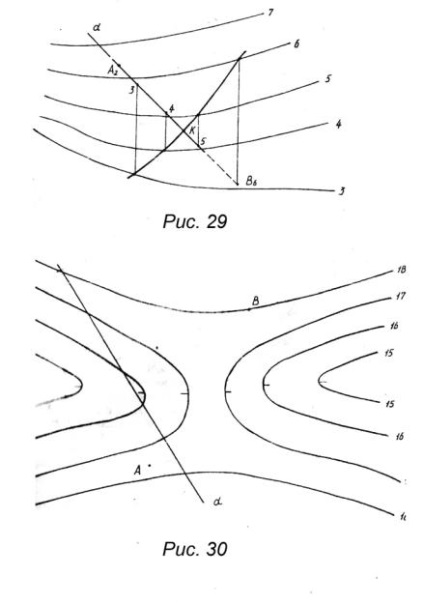
2. Проводити побудову лінії ската поверхні (рис. 27).
Наприклад, напрямок лінії найбільшого скату в точці D буде збігатися з напрямком перпендикуляра проведеного з цієї точки до сусідньої горизонталі в напрямку зменшення відміток (показано стрілкою). Визначення самої лінії найбільшого скату для довільної точки поверхні (в нашому випадку т. A) проводиться таким чином:
Опускаємо перпендикуляр на сусідню горизонталь (т. C). Так як поверхня криволинейна, то перпендикуляр, відновлений з т. C, в зворотному напрямку з вихідною точкою A не збіжиться, а виявиться в точці E. Бісектриса кута ACE дасть напрямок лінії найбільшого скату в найближчих до вихідної точки A точках поверхні. Для точки A лінію найбільшого ската проведемо паралельно бісектрисі кута ACE.
3. Визначити лінію перетину топографічної поверхні проецирующей площиною. Такий перетин (рис. 28, а, б) називається профілем поверхні. Січна площина задана своєю горизонтальною проекцією γ. Відзначивши точки перетину площини з горизонталями поверхні, побудуємо профіль поверхні. Для цього виберемо базову горизонталь відповідну, або трохи нижче, мінімальної позначки горизонталі місцевості, що перетинається площиною γ. Провівши перпендикулярно сліду площині лінії
зв'язку, відкладемо на них позначки відповідних горизонталей і з'єднаємо їх плавною кривою. Зазвичай масштаб, в якому відкладаються вертикальні позначки по лініях зв'язку, більше горизонтального масштабу. В цьому випадку отримується профіль більш виразний. На профіль наноситься сітка горизонталей. Перша горизонталь профілю називається базовою. Профіль може бути накладеним, як показано на малюнку 28, а, або винесеним (рисунок 28, б). У разі винесеного профілю він розташовується в довільному місці креслення з довільною орієнтацією щодо сліду січної площини (див. Зразок виконання графічного завдання).
4. Знаходити перетин прямої лінії з топографічною поверхнею (рис. 29). Дане завдання розбивається на наступні етапи:
а. Градуіруем задану пряму AB;
б. Укладаємо пряму в площину загального положення α; в. Знаходимо точки перетину горизонталей цій площині з горизонталями
топографічної поверхні (оскільки площину в яку укладаємо пряму має довільну орієнтацію, то горизонталі цій площині, залишаючись паралельні між собою, до прямої AB нахилені під довільним кутом);
м Поєднавши отримані точки плавною кривою, одержимо лінію перетину площини α і топографічної поверхні. У точці перетину цієї лінії і заданої прямої знаходиться шукана точка K перетину топографічної поверхні і прямої AB.
1. Що називається топографічної поверхнею?
2. Для чого призначені бергштрихи?
3. Яке припущення приймається про характер зміни місцевості між горизонталями?
4. Яка горизонталь носить назву базової при побудові профілю місцевості?
5. У чому відмінність побудови накладеного профілю місцевості від винесеного?
1. Визначити позначку проміжної точки A топографічної поверхні (рис. 30).
2. Побудувати лінію найбільшого ската поверхні, починаючи від точки B (рис. 30).
3. Побудувати профіль місцевості по заданому напрямку сліду січної площини α
2 ВКАЗІВКИ ДО ВИКОНАННЯ епюри
Накресливши рамку креслення і рамку основного напису, слід накреслити топографічний план ділянки місцевості, що відводиться під будівництво. Потім нанести на нього план земляної споруди. Масштаб креслення слід збільшити в три або чотири рази в порівнянні з масштабом завдання. Варіант завдання береться в додатку. Номер варіанта задається викладачем. На плані споруди потрібно вирішити такі завдання:
1. Побудувати лінії перетину укосів виїмок і насипів земляного споруди між собою.
2. Побудувати лінії перетину укосів виїмок і насипів земляного споруди з топографічною поверхнею.
3. Побудувати профіль місцевості і земляної споруди у напрямку А-A.
При оформленні завдання необхідно врахувати наступні вимоги:
1. Епюр виконується в олівці на аркуші креслярського паперу формату А3.
2. Горизонталі топографічної поверхні до кордону укосів проводять суцільними тонкими лініями, а в межах земляних робіт між схилами - штриховими лініями. Товщина ліній 0,1 ... 0,2 мм.
3. Контур земляного споруди і лінії перетину укосів з топографічною поверхнею викреслюють товщиною лінії 0,5 ... 0,6 мм.
4. бергштрихів на укосах виїмок і насипів проводять перпендикулярно горизонталях,
чергуються між собою
3. ПРИКЛАД ВИКОНАННЯ епюри
3.1. Визначення інтервалів укосів виїмки, насипи і дороги
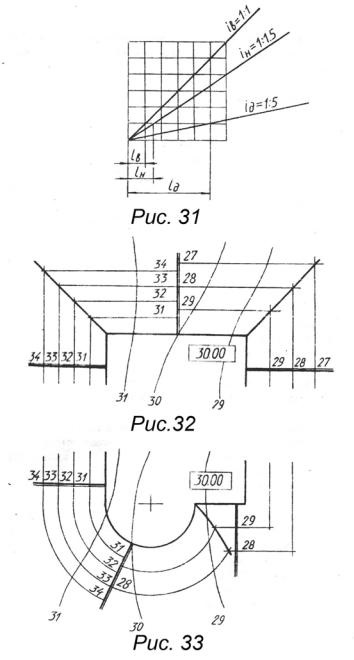
Прийнявши ухил укосів виїмок i в = 1: 1, ухил укосів насипів i н = 1: 1.5, ухил дороги i д = 1: 5, будуємо масштаб ухилів (рис. 31).
На вертикальній і горизонтальній прямій лінії, проведеної з однієї точки, будуємо лінії ухилів, відкладаючи необхідну кількість клітин по вертикалі і горизонталі. Наприклад, для побудови ухилу дороги відкладаємо одну клітку по вертикалі і п'ять по
горизонталі. При цьому на отриманому масштабі ухилів відзначаємо інтервали виїмки (ℓв), насипу (ℓ н) та дороги (ℓ д).
3.2. Побудова лінії перетину прямолінійних укосів земляної споруди
Для побудови лінії перетину укосів земляної споруди (рис. 32) встановлюємо лінію нульових робіт, яка пройде по 30-й горизонталі місцевості, тому що майданчик земляного споруди має позначку 30. Зліва від тридцятої горизонталі місцевості земляна споруда буде в виїмці, праворуч на насипу. Перпендикулярно кордонів майданчики будуємо масштаби ухилу укосів виїмки та насипу. Паралельно крайках майданчики проводимо горизонталі укосів з відмітками 27, 28, 29 і т. Д. Для насипу і 31, 32, 33 і т. Д. Для виїмки. Лінія перетину укосів проходить через точки перетину горизонталей, що мають однакові позначки.
3.3. Побудова лінії перетину прямолінійного і криволінійного укосів
Поверхня укосів, що обмежують майданчик півколом, являє собою частину конічної поверхні, горизонталями якої є концентричні півкола, центр яких збігається з центром півкола, що обмежує майданчик.
Побудова лінії перетину укосів (рис. 33) відбувається в наступній послідовності:
1. Перпендикулярно прямолінійним кордонів майданчики проводимо масштаби ухилу. Зліва від тридцятої горизонталі топографічної поверхні масштаб ухилу виїмки, праворуч - насипу.
2. Проводимо масштаби ухилів виїмки і насипу криволінійних укосів, спрямованих в центр.
3. Проводимо проектні горизонталі прямолінійних і криволінійних укосів з відмітками 27, 28 і т. Д. Для насипу і з відмітками 31, 32 і т. Д. Для виїмки. Через точки перетину прямолінійних і криволінійних горизонталей, що мають однакові позначки, проводимо лінії перетину укосів.
3.4. Побудова лінії перетину укосів майданчика і дороги
Укіс майданчики з пов'язаною з нею дорогою (рис. 36) розташовані на насипу. Горизонталі укосу площадки з відмітками 27, 28, 29 побудовані при визначенні лінії перетину укосів (рис. 32, 33).
Для побудови горизонталей укосів дороги, вісь яких прямолінійна, градуіруем полотно дороги. Від кромки майданчика з відміткою 30 відкладаємо по осі дороги інтервали ℓ д і проводимо горизонталі дороги.
З точок перетину горизонталей дороги з крайкою дороги проводимо окружності радіусом, рівним інтервалу ℓ н. які мають позначки 28,27, 26 і т. д. З точок перетину горизонталей дороги з її кромкою проводимо дотичні до кіл, які мають однакові позначки з точкою. Дотичні до кіл (рис. 34) є горизонталями укосу дороги. Через точки перетину однозначних горизонталей укосів майданчика і дороги проводимо лінії перетину укосів.
Якщо ділянку дороги вигнутий, то побудови нічим принципово не відрізняються від описаних, але горизонталями укосу дороги будуть плавні криві, дотичні до кіл з однаковими відмітками.