Екстраполяція - це метод наукового дослідження, який заснований на поширенні минулих і справжніх тенденцій, закономірностей, зв'язків на майбутній розвиток об'єкта прогнозування. До методів екстраполяції відносяться метод ковзної середньої, метод експоненціального згладжування, метод найменших квадратів.
Метод експоненціального згладжування найбільш ефективний при розробці середньострокових прогнозів. Він прийнятний при прогнозуванні тільки на один період вперед. Його основні переваги простота процедури обчислень і можливість обліку ваг вихідної інформації. Робоча формула методу експоненціального згладжування:
де t - період, що передує прогнозному; t + 1 - прогнозний період; Ut + 1 - прогнозований показник; # 945; - параметр згладжування; Уt - фактичне значення досліджуваного показника за період, що передує прогнозному; Ut - експоненціально зважена середня для періоду, що передує прогнозному.
При прогнозуванні даним методом виникає два утруднення:
- вибір значення параметра згладжування # 945 ;;
- визначення початкового значення Uo.
від величини # 945; залежить. як швидко знижується вага впливу попередніх спостережень. Чим більше # 945 ;, тим менше позначається вплив попередніх років. якщо значення # 945; близьке до одиниці, то це призводить до врахування при прогнозі в основному впливу лише останніх спостережень. якщо значення # 945; близьке до нуля, то ваги, по яких зважуються рівні тимчасового ряду, убувають повільно, тобто при прогнозі враховуються всі (або майже всі) минулі спостереження.
Таким чином, якщо є впевненість, що початкові умови, на підставі яких розробляється прогноз, достовірні, слід використовувати невелику величину параметра згладжування (# 945; → 0). Коли параметр згладжування малий, то досліджувана функція поводиться як середня з великого числа минулих рівнів. Якщо немає достатньої впевненості в початкових умовах прогнозування, то слід використовувати велику величину # 945 ;, що призведе до обліку при прогнозі в основному впливу останніх спостережень.
де n - число спостережень, що входять в інтервал згладжування.
Завдання вибору Uo (експоненціально зваженого середнього початкового) вирішується наступними способами:
- якщо є дані про розвиток явища в минулому, то можна скористатися середньої арифметичної і прирівняти до неї Uo;
- якщо таких відомостей немає, то в якості Uo використовують вихідне перше значення бази прогнозу У1.
Також можна скористатися експертними оцінками.
Відзначимо, що при вивченні економічних часових рядів і прогнозуванні економічних процесів метод експоненціального згладжування не завжди «спрацьовує». Це обумовлено тим, що економічні часові ряди бувають занадто короткими (15-20 спостережень), і в разі, коли темпи зростання і приросту великі, даний метод не «встигає» відобразити всі зміни.
Приклад застосування методу експоненціального згладжування для розробки прогнозу
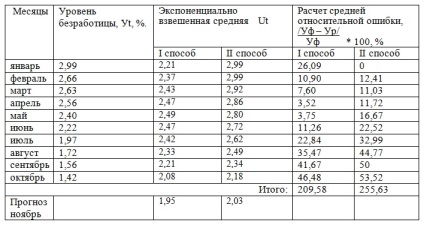
Завдання. Є дані, що характеризують рівень безробіття в регіоні,%
Рішення методом експоненціального згладжування
1) Визначаємо значення параметра згладжування за формулою:
де n - число спостережень, що входять в інтервал згладжування. # 945; = 2 / (10 + 1) = 0,2
2) Визначаємо початкове значення Uo двома способами:
І спосіб (середня арифметична) Uo = (2,99 + 2,66 + 2,63 + 2,56 + 2,40 + 2,22 + 1,97 + 1,72 + 1,56 + 1,42) / 10 = 22,13 / 10 = 2,21
II спосіб (приймаємо перше значення бази прогнозу) Uo = 2,99
3) Розраховуємо експоненціально зважену середню для кожного періоду, використовуючи формулу
де t - період, що передує прогнозному; t + 1 - прогнозний період; Ut + 1 - прогнозований показник; # 945; - параметр згладжування; Уt - фактичне значення досліджуваного показника за період, що передує прогнозному; Ut - експоненціально зважена середня для періоду, що передує прогнозному.