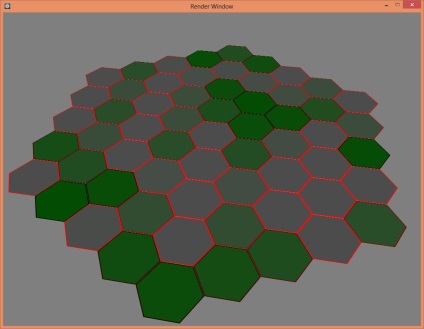
Доброго дня. Нещодавно я зіткнувся з проблемою генерації шестикутної сітки з центру. Є методи генерації рядками. Вони придатні для будь-чого. А такого методу я не знайшов. Може погано шукав, хто знає. На форумі мені запропонували три кривих рішення:
1. Милиці (варіант, який найгірший).
2. Генерація по рядках та викидання непотрібного. В принципі найправильніше рішення, але на жаль, мені потрібно щоб саме з центру. Потім зручно додавати потрібні комірки буде.
3. Косі координати. Це складна мегажесть, на яку можна вбити хмару часу. Я її не зміг осилити.
А тепер, перейдемо до нашого алгоритму.
Суть на пальцях
Нам потрібно отримати комірчастуструктуру аля ця.
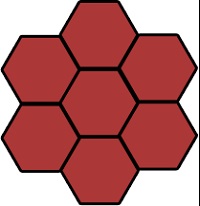
Першим кроком буде генерація першого, центрального гексагона.
Якщо наш глядач досить прозорливий, то він помітить, що прилягають по сторонам осередки утворюють осі матриці.
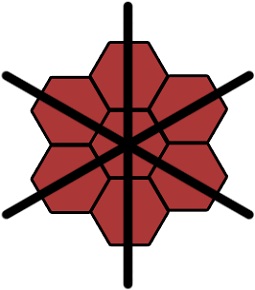
З першим рядом проблем не виникне, якщо знати радіус і кут, то все шестикутники ляжуть як треба. Проблеми йдуть з другим рядом. Деякі вічка не будуть лежати де треба. А причина в наступному. У нашій структурі, є періодичність. Але вона не кругова, а гексагональна. Просто в першому ряду вони сходяться.
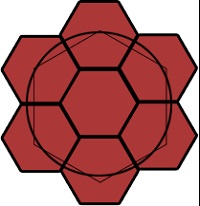
На малюнку видно, що центри шестикутників лежати і на окружності, і на матричному шестикутнику. Однак на другому ряду проблема видна чітко.
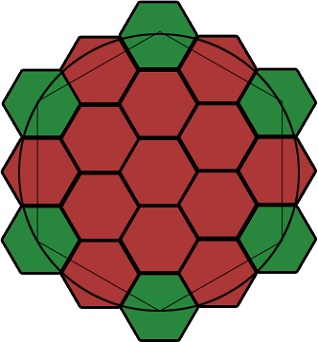
Видно, що на лише осьові шестикутники (зелені) лежать на окружності. Центри інших зміщені до центру і лежать на матричному шестикутнику. Тому, через радіальну симетрію таку сітку не поставити.
Звідси випливає наступне рішення.
Будуємо спочатку лише осьові шестикутники.
Потім обчислюємо вектори. На малюнку вказано напрямок векторів. Воно може бути зворотним.
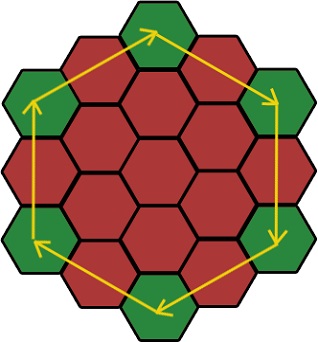
Але нам потрібен не цей вектор. Точніше не він сам, а його частина.
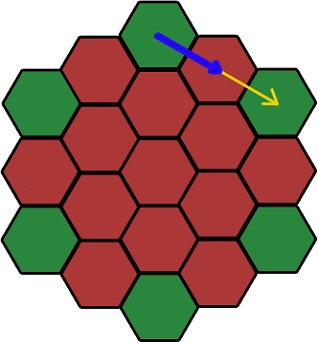
Нам потрібен синій вектор. Цей зсув, яке додається до осьового шестикутник для отримання точних координат. Жовтий вектор ділиться на число частин, рівну кількість шестикутників між осьовими шестикутниками + 1 (або номер шару).
Після цього, можна генерувати як завгодно великі матриці з центру.
А тепер наведу код, цього неподобства. Я програмував на Xors3D, але думаю, що кому треба, той зрозуміє як ця штука працює (тим більше, код простий, а суть пояснив вище). Нам потрібна всього одна функція - функція створення осередку.
Ось її код.
; Vector calculating
If Order> 0 Then - обчислюємо вектора, якщо ряд не нульовий (де центральний гексагон)
Vector (i, 0) = ((CellRadius * Sin (Angle + 60) * Order-CellRadius * Sin (Angle) * Order)) / (Order) - 0 = X, перша координата вектора
Vector (i, 1) = ((CellRadius * Cos (Angle + 60) * Order-CellRadius * Cos (Angle) * Order)) / (Order) - 1 = Z, друга координата вектора
End If
Next
Що маємо на виході:
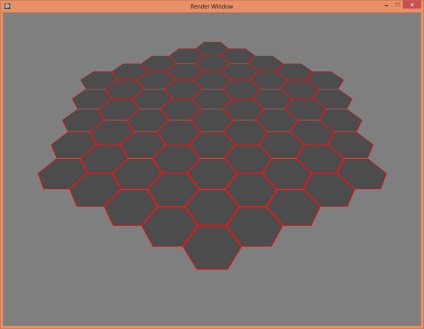
Апгрейд 1.0 - Поворот на будь-який кут матриці
Можуть виникнути ситуації, коли нашу гексагональную сітку треба кудись примкнути під потрібним кутом. Я подумав над цим, і модернізованих функцію - тепер можна повертати всю матрицю на довільний кут!
Отже, код:
Важливі відмінності:
Function CreateCell (X #, Z #, Order%, AddAngle%) - з'явився новий аргумент, це і є довільний кут - AddAngle.
Angle # = 360 / Limit * i + AddAngle - додаємо зсув для розрахунку кутів і векторів.
xRotateEntity Cell \ Sprite, 90, -AddAngle, 0 - поворот спрайту навколо вертикальної осі в протилежну сторону.
Що маємо на виході:
17 градусів.
30 градусів.
10 градусів.