Події. Операції над подіями
Під подією в теорії ймовірностей розуміється всякий факт, який в результаті досвіду може відбутися або не відбутися.
А - з'явився герб при киданні монети;
В - поява трьох гербів при триразовому киданні монети;
З - влучення в ціль при пострілі;
D - поява туза, якщо вийняти картку з колоди; і т.д.
Розглядаючи перераховані вище події, ми бачимо, що кожне з них має якусь ступенем можливості: одні - більшою, інші - меншою. Причому, для деяких подій ми відразу ж можемо вирішити, яке з них більше, а яке менше можливо. Щоб кількісно порівняти між собою події за ступенем їх можливості, очевидно потрібно з кожним подією зв'язати певне число, яке тим більше, чим більш можливо подія. Таке число ми називаємо ймовірністю події.
Розглянемо безліч подій М, які можна спостерігати в деякому експерименті. Виділимо, насамперед, два спеціальних події - достовірна подія - U, яке обов'язково відбувається в експерименті, і неможлива подія - V, яке не може відбутися в експерименті ніколи.
Для кожної події А з М введемо протилежне подія А, яке полягає в тому, що подія А не відбулося.
Подія ∪, що полягає в тому, що з двох подій А і В відбувається принаймні одне (або А, або В, або А і В разом), називається сумою (або об'єднанням) подій А і В.
Подія ∩, що полягає в тому, що події А і В відбуваються одночасно, називається твором (або перетином) подій А і В.
Подія A \ B називається різницею подій А і В; воно полягає в тому, що відбувається А і не відбувається В.
Операції над подіями мають наступні властивості:
- і - коммутативность додавання і множення;
- і - асоціативність додавання і множення;
- - закони дистрибутивности.
елементарні результати
Припустимо, що серед усіх можливих подій A, які в даному досвіді з волі випадку відбуваються або не відбуваються, можна виділити сукупність так званих елементарних подій або елементарних фіналів. що володіють такими властивостями:
- по-перше, всі вони взаємно виключають одна одну, тобто є непересічними;
- по-друге, в результаті даного досвіду обов'язково відбувається одне з цих елементарних подій;
- по-третє, яке б не була подія A, по наступило елементарного результату завжди можна судити про те, чи відбувається або не відбувається ця подія.
Елементарні результати зазвичай позначаються грецькою буквою ω, а їх сукупність Ω називається простором елементарних подій.
Достовірна подія U, що настає в результаті будь-якого з елементарних фіналів ω, при такому ототожненні подій безліччю збігається з простором: U = Ω.
Неможливе подія V, що не наступає ні при якому елементарному результаті ω, збігається з порожнім безліччю і позначається: V = Ø.
Дві події А і В несумісні (або несумісні), якщо А∩В = Ø (тобто подія неможливо).
Події - утворюють повну групу подій, якщо вони попарно несумісні і ∪∪∪ ... ∪, тобто з цих подій відбувається одне й тільки одне.
ПРИКЛАД 1. Переможець змагання нагороджується: призом (подія А), грошовою премією (подія В), медаллю (подія С). Що являють собою події: а) А + В; б) АВС; вас в?
а) Подія А + В полягає в тому, що переможець нагороджений призом, або премією, або призом і премією одночасно.
б) Подія ABC полягає в тому, що переможець нагороджений призом, премією та медаллю одночасно.
в) Подія АС-В складається у нагородженні переможця призом і медаллю одночасно, без видачі премії.
Для наочної ілюстрації алгебри подій скористаємося діаграмами Ейлера - Венна.
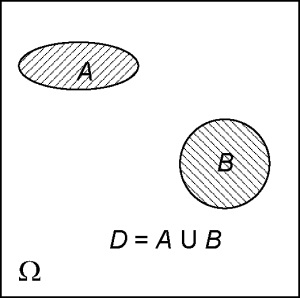
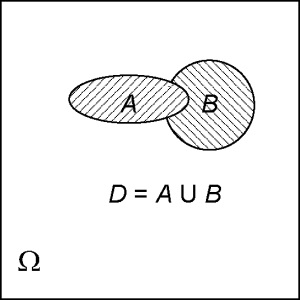
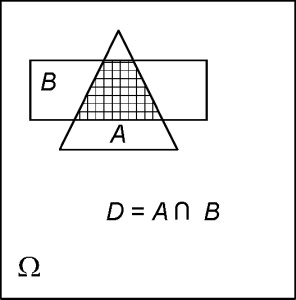
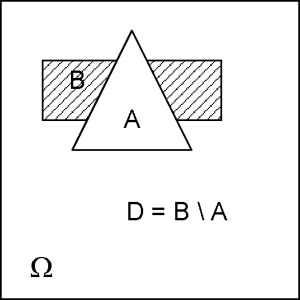
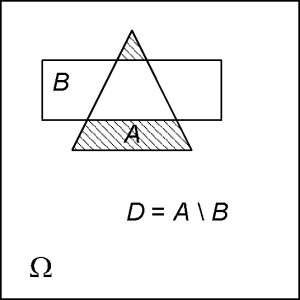
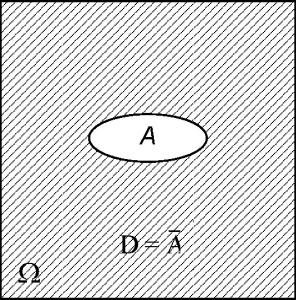
Тут кожній картинці (прямокутника) відповідає простір елементарних подій Ω.
ПРИКЛАД 9. Описати простір елементарних подій наступного досвіду. Кинуті дві гральні кістки.
Рішення. Очевидно, елементарним результатом даного досвіду можна вважати пару чисел ω = (a, b), де а - число очок на першій костіb - число очок на другий кістки. Відомо, що (1 ≤ a, b ≤ 6), причому кількість очок на першій кістки не залежить від того, скільки очок випаде на другий кістки і навпаки. Звідси отримаємо:
На цьому я закінчую, тому що по даній темі мені доповнити вже нічого. Всім дякую за увагу!