Asix Адмін. відповів 8 місяців тому
Радіус вписаного кола в ромб
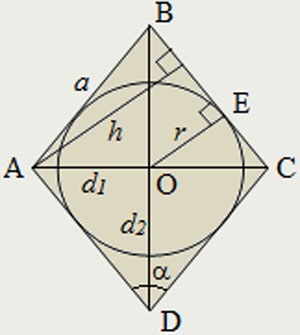
Існує властивість кола, яку можна вписати в чотирикутник. Для цього має виконуватися за все одна умова: сума однієї пари протилежних сторін повинна дорівнювати сумі іншої пари протилежних сторін.
Оскільки для ромба ця умова виконується, то окружність можна вписати в будь-який ромб. Центр вписаного кола і точка перетину діагоналей ромба збігаються.
Розглянемо кілька способів обчислення радіуса вписаного в ромб кола
1 варіант. Обчислити радіус вписаного кола через висоту.
Оскільки висота ромба і діаметр вписаного кола рівні, що випливає з властивостей прямокутника, утвореного діаметром вписаного кола і висотою ромба.
Запишемо формулу радіуса вписаного кола:
2 варіант. Обчислити радіус вписаного кола через діагоналі.
Розглянемо формулу площі ромба через радіус вписаного кола:
З іншого боку площа ромба можна знайти через діагоналі:
Прирівняємо праві частини записаних формул площ і отримаємо:
З цієї рівності висловимо радіус: