У Стародавній Греції коло і окружність вважалися вінцем досконалості. Дійсно, в кожній своїй точці коло влаштована однаковим чином, що дозволяє їй рухатися самої по собі. Це властивість кола зробило можливим виникнення колеса, оскільки вісь і втулка колеса повинні весь час бути в контакті.
У школі вивчається багато корисних властивостей кола. Однією з найкрасивіших теорем є наступна: проведемо через задану точку пряму, що перетинає задану окружність, тоді твір відстаней від цієї точки до
точок перетину кола з прямою не залежить від того, як саме була проведена пряма. До цієї теореми близько двох тисяч років.
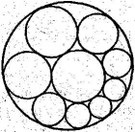
На рис. 2 зображені дві окружності і ланцюжок кіл, кожна з яких стосується цих двох кіл і двох сусідів по ланцюжку. Швейцарський геометр Якоб Штейнер близько 150 років тому довів наступне твердження: якщо при деякому виборі третьої окружності ланцюжок замкнеться, то вона замкнеться і при будь-якому іншому виборі третьої окружності. Звідси випливає, що якщо одного разу ланцюжок не замкнулася, то вона не замкнеться при будь-якому виборі третьої окружності. Художнику, которий малював зображену ланцюжок, довелося б чимало потрудитися, щоб вона вийшла, або звернутися до математику для розрахунку розташування двох перших кіл, при якому ланцюжок замикається.
Спочатку ми згадали про колесі, але ще до колеса люди використовували круглі колоди - катки для перевезення вантажів.
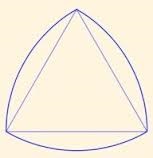
Виберіть вірні твердження, виходячи з малюнка:
1) Точки C, B і E не належать колу.
2) Точки D, B і O належать окружності.
3) Точки A, B і O належать колу.
Невірно. Точка B належать кругу, так як окружність частина кола. Невірно. Точка O центр кола, але не лежить на ній.
1) Точка О є центром і окружності, і кола.
2) Точка О є центром кола, але не центром кола.
3) Точки D і B не належать окружності.
1) Точки B і D не належать колу.
2) Точки A, B, D і O належать колу.
3) Точки B, D і E належать колу.
Невірно. Точка О є центром і окружності, і кола. Невірно. Точки D і B належать окружності. Невірно. Точки B і D належать колу, так як лежать на окружності, а вона частина кола.
1) Точки B і D поділяють коло на 4 дуги.
2) Точки B і D поділяють коло на 3 дуги.
3) Точки B і D поділяють коло на 2 дуги.
Невірно. Точка E не належать колу, так як знаходиться за його межами. Невірно. Точки B і D поділяють коло на 2 дуги. Невірно. Точки B і D поділяють коло на 2 дуги. Нeвeрнo. Завдання виконано.
Коло і окружність - одні з найдавніших геометричних фігур, філософи давнини надавали їм велике значення. Коло - втілення нескінченного Часу і Простору, символ всього сущого, Всесвіту. "З усіх фігур найвродливіша - коло", - вважав Піфагор.
Навколо нас багато круглих предметів. Уявіть собі на секунду, що раптом трапилася біда: на Землі зникло все кругле! Здавалося б - нехай все буде квадратним. Хіба не можна прожити без круглих труб, а до квадратних колесам не можна звикнути? Чи можна взагалі уявити життя людини без використання кола? Чому так багато тіл мають круглу форму? Щоб знайти відповіді на всі ці питання, в першу чергу, необхідно розглянути історію виникнення цих понять і подальший їх розвиток.
Історія виникнення і розвитку геометричних понять
Для первісних людей важливу роль грала форма їхніх околицях предметів. За формою і кольором вони відрізняли їстівні гриби від неїстівних, придатні для будівель породи дерев від тих, які годяться лише на дрова, смачні горіхи від гірких і т.д. Особливо смачними здавалися їм горіхи кокосової пальми, схожі на кулю. Спеціальних назв для геометричних фігур, звичайно, не було. Говорили: "такий же, як кокосовий горіх" або "такий же, як сіль" і т.д. Так, опановуючи навколишнім світом, люди знайомилися з найпростішими геометричними фігурами.
Круглі тіла ще в давнину зацікавили людини. У Стародавньому Єгипті для побудови знаменитих єгипетських пірамід ніяких технічних споруд ще не було. Навіть шліфувати величезні кам'яні брили доводилося вручну, а переміщували їх за допомогою колод круглої форми. Помітили, що перекочування простіше, якщо взяти шматок дерева з майже однаковою товщиною на початку і в кінці. Так люди познайомилися з одним з найважливіших тел - циліндром. Скалками циліндричної форми користувалися і жінки, розгортаючи білизна після прання. Перевозити вантажі на ковзанках було досить важко, тому що самі стовбури дерев важили багато. Щоб полегшити роботу, стали вирізати зі стовбурів тонкі круглі пластинки, які котилися вже легше і з їх допомогою перетягували вантажі. Так з'явилося перше колесо. На жаль, невідомий безпосередній винахідник колеса.
Не тільки в процесі роботи люди знайомилися з різними фігурами. З давніх-давен вони любили прикрашати себе, свій одяг, своє житло. І багато, створені давним-давно прикраси, мали ту чи іншу форму. Намисто були кулястими, браслети і кільця мали форму кола. Стародавні майстри навчилися надавати красиву форму бронзі, золоту, сріблу, коштовних каменів. Художники, розписували палаци, теж використовували коло. З часу винаходу гончарного круга люди навчилися робити круглу посуд - горщики, вази, амфори. Круглими були і колони, що підпирають будівлі.
Математичні знання єгиптян і вавилонян були розрізнені і представляли собою звід правил, перевірених практикою. У Стародавній Греції все розрізнені знання привели в систему, геометрія стала бурхливо розвиватися як наука. Тільки в Стародавній Греції "окружність" і "коло" отримали свої назви, майже всі назви геометричних фігур грецького походження, як і саме слово геометрія ( "гео" - земля, а "Метро" - міряти). Однак ці слова увійшли в російська мова не безпосередньо з грецького, а через латинську мову.
У Стародавній Греції багато властивостей фігур, в тому числі кола і кола були сформульовані у вигляді теорем і доведені. Найбільш вдало була викладена геометрія, як наука про властивості геометричних фігур, грецьким вченим Евклідом (III в. До н. Е.) В своїх книгах "Почала". Протягом багатьох століть "Почала" були єдиною навчальною книжкою, по якій молодь вивчала геометрію. І навіть зараз, в наш час, підручники написані під великим впливом "Почав" Евкліда.
Коло і круг - це плоскі фігури. Ми живемо в світі трьох вимірів. А в яке геометричне тіло перетворяться окружність і коло, якщо потраплять в простір? Це сфера і куля. "Сфера" - походить від грецького слова "сфайра", в перекладі - "м'яч". Крім цього геометрія простору розглядає і інші круглі тіла - це "циліндр" (від грецького слова "кюліндрос", що означає "валик", "каток") і "конус" (від грецького слова "Коносу", що означає "соснова шишка") . Найважливішим серед круглих тел був куля.
Отже, в Стародавній Греції коло і окружність вважали вінцем досконалості. "У кожній своїй точці коло влаштована однаковим чином, що дозволяє їй рухатися самої по собі". Це властивість кола стало поштовхом до виникнення колеса. .
Коло - "ціркулус" - латинське слово, від нього ж і "циркуль", без якого б ми не побудували коло. Циркуль і лінійка - найстаріші креслярські інструменти на Землі.
Елементи окружності і кола:
- це відрізок, що з'єднує центр кола з будь-якій її точкою (по-латині - спиця колеса).
Діаметр кола - це хорда, що проходить через центр кола (з грецької - "діаметр").
Хорда кола - відрізок, що з'єднує будь-які дві точки на колі (з греческого- "струна").
Дуга кола - це частина окружності, обмежена двома точками.
Часто в практичних завданнях потрібно дізнатися довжину кола. А як виміряти довжину окружності, якщо сама окружність - крива лінія, а одиниця вимірювання довжини - відрізок? Є кілька способів вимірювання довжини кола.
Однак ці способи безпосереднього вимірювання довжини окружності малоудобна і дають наближені результати. Тому вже з давніх часів почали шукати більш досконалі способи вимірювання довжини кола. В процесі вимірювань помітили, що між довжиною кола і довжиною її діаметра є певна залежність: З: d ≈ 3,1.
Багато вчених - математики намагалися довести, що це ставлення є число постійне, яке не залежить від розмірів окружності, його стали позначати грецькою буквою π-ο ерша буква грецького слова "периферія" - круг.
З: d = π, де С - довжина кола, d - довжина діаметра, звідси і формула довжини кола C = πd або C = 2πr.
Вивчивши дослідження вчених математиків, ми провели такі виміри й обчислення:
1. Обчислення числа пі. а) за допомогою тонкої нитки виміряли довжину кола С деяких предметів побуту; б) щоб точніше визначити довжину диметра d, доклали цей предмет до аркуша паперу і обвели олівцем, вирізали, згорнули навпіл, лінія згину - це діаметр, виміряли його за допомогою лінійки; в) знайшли ставлення З: d, дані занесли в таблицю:
Довжина кола С
2. Межі значення числа пі. а) за допомогою циркуля вписали коло в квадрат: якщо діаметр дорівнює 1, то довжина кола дорівнює π. Периметр квадрата зі стороною 1 дорівнює 4. Отже π менше 4. (. Рис.1). б) в цей же коло вписали правильний шестикутник: діаметр кола знову 1, довжина кола дорівнює π. Сторона правильного шестикутника дорівнює радіусу, т.е.0,5, а периметр дорівнює 6 · 0,5 = 3, отже π більше 3 (. Рис.2).
В результаті ми переконалися, що відношення довжини кола до його діаметру (число π) є число постійне і 3 <π <4, тобто. ми підтвердили дослідження вчених - математиків.
π -3,141 592 653 589 793 238 462 643 383279 502 884197 169 399 375 105 ....
Навіщо потрібно π, та ще з такою точністю? Число π надзвичайно важливо для вчених і інженерів. Все, що кругле і все, що рухається по колу (як колеса або планети), містить π. Без π люди не могли створити автомобілі, зрозуміти рух планет або порахувати скільки гороху поміститься в консервну банку. Але загадка таємничого числа не дозволена аж до сьогоднішнього дня, і, як і раніше, хвилює вчених. В даний час з числом π пов'язано труднообозримой безліч формул, математичних і фізичних фактів. Їх кількість продовжує стрімко зростати. Все це говорить про зростаючий інтерес до найважливішої математичної константі, вивчення якої налічує вже понад двадцять двох століть.
Вивчивши літературу і виконавши власні вимірювальні дослідження з окружністю і колом, ми прийшли до наступних висновків: окружність і коло - це дивно гармонійні фігури. Окружність - єдина крива, яка може "ковзати сама по собі", обертаючись навколо центру. Це властивість кола дає відповідь на питання, чому для її креслення використовують циркуль, і чому колеса роблять круглими, а не квадратними або трикутними.
Коло в нашому житті.
Досліджуючи питання про роль кола в нашому житті, ми провели анкетування учнів 5-9 класів та педагогів МО ШІСП (всього 90 осіб):- Які круглі тіла ви зустрічаєте в нашому житті?
- Яке значення має коло в інших науках?
- Які практичні завдання повсякденному житті вирішуються, використовуючи знання про коло і окружності?
- Як ви вважаєте, чому зустрічається так багато круглих тел в природі?
Відповіді на перше питання представлені в.
З відповідей вчителів - предметників на друге питання анкети ми зрозуміли, що коло має велике значення не тільки в математиці, але і в інших науках: