Завдання з тригонометрії є невід'ємною частиною будь-якого серйозного іспиту. Рідкісна підготовка до ЄДІ з математики обходиться без уваги репетитора до цього об'ємного і складного розділу. З ним пов'язана найбільша кількість помилок провалів на ЄДІ у слабких абітурієнтів. Розглянемо методичні особливості вивчення тригонометрії і приватні прийоми, якими зазвичай користується репетитор з математики. Я збираюся зробити кілька сторінок з цієї тематики. На початку поговоримо про введення тригонометричного кола.
На жаль, стандарти ДПА з математики змусили переглянути шкільні програми, в які в цьому році були внесені істотні зміни. Традиційно досліджувану в 9 класі тригонометрію замінили на статистику і теорію ймовірностей. Репетитору математики це тільки ускладнило роботу. Звичайно, і раніше атестаційний іспит з алгебри торкався синуси і косинуси, але принаймні введення в тригонометрію вивчалося. Тепер все змінилося на корені і «старт» доводиться брати в 10 класі. Для репетитора це означає поєднання дворічної підготовки до ЄДІ з навчанням роботі на тригонометричному колі з нуля. Але робити нічого, доводиться адаптуватися до нових стандартів і підручниками. Отже, які методичні прийоми пропонує репетитор з математики школяреві в цій темі? Наскільки різним може бути підхід до введення кола? Як побудувати роботу зі слабким учнем?
Вивчення тригонометрії починається з вимірювання і відкладання кутів. І вже на цьому етапі репетитор з математики може зіткнутися з певними проблемами. З чим вони пов'язані? Зазвичай плутають розташування кутів на колі і не бачать його в «розкритому стані». У жодному підручнику я ще не зустрічав того, що говорю своїм учням. Давайте подивимося на малюнок кола. Що це таке? В очах учня це обмежена замкнута лінія, на якій репетитор з математики завдає якісь числа і букви, оголошуючи їх кутами. Біля однієї і тієї ж точки підписується відразу кілька різних значень. Що це? Ще й радіани замість звичних градусів. Плутанина виникає страшна. Особливо коли репетитор з математики переходить до вирішення найпростіших тригонометричних рівняння (це тема в підручнику Мордкович йде мало відразу за тригонометричним колом). Як внести ясність в те, що відбувається?
Методика спіралі репетитора з математики
Я завжди «розмотувати» тригонометричний коло. Як? Що це за дійство? Все дуже просто. Пояснюю так: «кути, як і довжини відрізків, відкладаються (зображуються) на нескінченній осі. Тільки для практичної роботи з процесом зображення зручніше змотати цю вісь петлями, або, кажучи іншими словами, представити її у вигляді спіралі ». І показую малюнок:
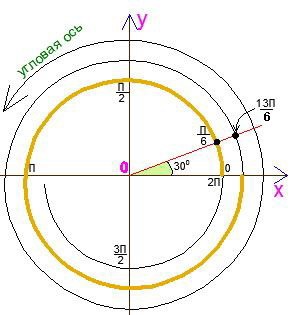
При такому підході репетитор з математики забезпечує повну прозорість дій з кутами і ясність в їх зображенні. Щоб спростити роботу учня з колом потрібно подати його як вісь для кутів, яку як мотузку намотали на трубу і намалювали вийшла профіль. Така методика допомагає репетитора з математики зняти величезну кількість проблем не тільки на етапі введення самого кола, а й на наступних уроках. особливо в рішенні рівнянь і нерівностей, коли доводиться записувати цілу серію кутів, що зображують однією і тією ж точкою або дуги, накладені один на одного. Я раджу репетитора виділити кольором частина кола, що відповідає одному обороту (на малюнку вона показана коричневим кольором) і назвати її «доріжкою».
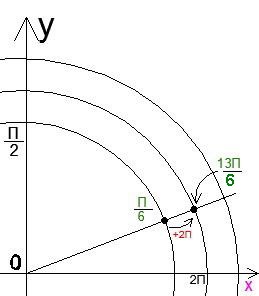
Учень повинен засвоїти, що малюнок підручника - картинка затягнутою спіралі, як ніби трубу щільно обмотали мотузкою. В такому випадку різні позначки (ділення) осі (тобто мотузки) будуть накладені один на одного і ми побачимо що позначки різних кутів зливаються в одну точку. Якщо ми послабимо мотузку, то отримаємо спіраль, на якій кожен кут зображується окремо.
У ті моменти, коли репетитор з математики відчуває нерозуміння і плутанину з кутами на допомогу приходить зображення кола в спіральному вигляді. Наприклад, рішення тригонометричного рівняння можна показати так:
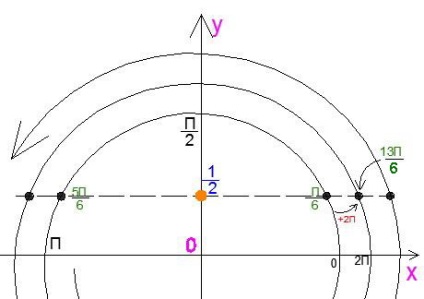
Необхідно сказати, що чорні точки (кути) - це і є рішення рівняння. І якщо ми стиснемо спіраль (затягнемо мотузку на трубі), то вони накладуться один на одного і перетворяться в ліву і праву. Після цього репетитор може зробити стандартний малюнок. Таким шляхом викладачеві буде легше пояснити формули і. а учень краще запам'ятає періодичний характер розташування коренів.
Олександр Миколайович, репетитор з математики Москва, м. Строгино