Кілька місяців тому я отримав від одного такого листа:
Тема: Чи можеш розгорнути і пояснити мені цю одну сходинку коду?
Текст: Вважай мене тупим, але ... я не розумію її і буду вдячний, якщо растолкуешь докладно. Це трассировщик променів в 128 символах. Мені здається, він чудовий.
index.html
Я помітив, що там змінна k - просто константа, так що прибрав її з рядка і перейменував в delay.
code.js
var delay = 64;
var draw = «for (n + = 7, i = delay, P = 'p. \ n'; i- = 1 / delay; P + = P [i% 2? (i% 2 * j-j + n / delay ^ j) 1: 2]) j = delay / i; p.innerHTML = P »;
var n = setInterval (draw, delay);
Далі, var draw був просто рядком, яка виконувалася як функція eval з періодичністю setInterval, оскільки setInterval може приймати і функції, і рядки. Я переніс var draw в явну функцію, але зберіг початкову рядок для довідки про всяк випадок.
var delay = 64;
var p = document.getElementById ( «p»); // <—————
// var draw = «for (n + = 7, i = delay, P = 'p. \ N'; i- = 1 / delay; P + = P [i% 2? (I% 2 * j-j + n /delay^j)1:2])j=delay/i;p.innerHTML=P »;
var draw = function () for (n + = 7, i = delay, P = 'p.n'; i - = 1 / delay; P + = P [i% 2. (i% 2 * j - j + n / delay ^ j) 1. 2]) j = delay / i; p.innerHTML = P;
>
>;
var n = setInterval (draw, delay);
Потім я оголосив змінні i, p і j і переніс їх в початок функції.
var delay = 64;
var p = document.getElementById ( «p»);
// var draw = «for (n + = 7, i = delay, P = 'p. \ N'; i- = 1 / delay; P + = P [i% 2? (I% 2 * j-j + n /delay^j)1:2])j=delay/i;p.innerHTML=P »;
var draw = function () var i = delay; // <—————
var P = 'p.n';
var j;
for (n + = 7; i> 0; P + = P [i% 2. (i% 2 * j - j + n / delay ^ j) 1. 2]) j = delay / i; p.innerHTML = P;
i - = 1 / delay;
>
>;
var n = setInterval (draw, delay);
Я розклав цикл for і перетворив його в цикл while. З трьох частин колишнього for залишилася тільки одна частина CHECK_EVERY_LOOP, а все інше (RUNS_ONCE_ON_INIT; DO_EVERY_LOOP) переніс за межі циклу.
var delay = 64;
var p = document.getElementById ( «p»);
// var draw = «for (n + = 7, i = delay, P = 'p. \ N'; i- = 1 / delay; P + = P [i% 2? (I% 2 * j-j + n /delay^j)1:2])j=delay/i;p.innerHTML=P »;
var draw = function () var i = delay;
var P = 'p.n';
var j;
n + = 7;
while (i> 0) // Update HTML
p.innerHTML = P;
j = delay / i;
i - = 1 / delay;
P + = P [i% 2. (i% 2 * j - j + n / delay ^ j) 1. 2];
>
>;
var n = setInterval (draw, delay);
Тут я розгорнув трійчастий оператор (condition. Do if true. Do if false) in P + = P [i% 2. (i% 2 * j - j + n / delay ^ j) 1. 2] ;.
Це значення (індекс) використовується для зсуву рядка P, так що назвемо index і перетворимо рядок в P + = P [index] ;.
var delay = 64;
var p = document.getElementById ( «p»);
// var draw = «for (n + = 7, i = delay, P = 'p. \ N'; i- = 1 / delay; P + = P [i% 2? (I% 2 * j-j + n /delay^j)1:2])j=delay/i;p.innerHTML=P »;
var draw = function () var i = delay;
var P = 'p.n';
var j;
n + = 7;
while (i> 0) // Update HTML
p.innerHTML = P;
j = delay / i;
i - = 1 / delay;
let index;
let iIsOdd = (i% 2! = 0); // <—————
P + = P [index];
>
>;
var n = setInterval (draw, delay);
Я розклав 1 з значення index = (i% 2 * j - j + n / delay ^ j) 1 в ще один оператор if.
Тут хитрий спосіб перевірки на парність результату в круглих дужках, коли для парного значення повертається 0, а для непарного - 1. - це побітовий оператор AND. Він працює так:
1 1 = 1
0 1 = 0
Отже, something 1 перетворює «something» в двійкове подання, а також добиває перед одиницею необхідну кількість нулів, щоб відповідати розміру «something», і повертає просто результат AND останнього біта. Наприклад, 5 в довічним форматі дорівнює 101, так що якщо ми застосуємо на ній логічну операцію AND з одиницею, то вийде наступне:
0 1 // 0 - even return 0
1 1 // 1 - odd return 1
2 1 // 0 - even return 0
3 1 // 1 - odd return 1
4 1 // 0 - even return 0
5 1 // 1 - odd return 1
Зверніть увагу, що я також перейменував решту index в magic, так що код з розгорнутим 1 буде виглядати наступним чином:
var delay = 64;
var p = document.getElementById ( «p»);
// var draw = «for (n + = 7, i = delay, P = 'p. \ N'; i- = 1 / delay; P + = P [i% 2? (I% 2 * j-j + n /delay^j)1:2])j=delay/i;p.innerHTML=P »;
var draw = function () var i = delay;
var P = 'p.n';
var j;
n + = 7;
while (i> 0) // Update HTML
p.innerHTML = P;
j = delay / i;
i - = 1 / delay;
let index;
let iIsOdd = (i% 2! = 0);
P + = P [index];
>
>;
var n = setInterval (draw, delay);
Далі я розгорнув P + = P [index]; в оператор switch. До цього моменту стало зрозуміло, що index може приймати тільки одне з трьох значень - 0, 1 або 2. Також зрозуміло, що змінна P завжди ініціалізується зі значеннями var P = 'p.n' ;, де 0 вказує на p, 1 вказує на. а 2 вказує на n - символ нового рядка
var delay = 64;
var p = document.getElementById ( «p»);
// var draw = «for (n + = 7, i = delay, P = 'p. \ N'; i- = 1 / delay; P + = P [i% 2? (I% 2 * j-j + n /delay^j)1:2])j=delay/i;p.innerHTML=P »;
var draw = function () var i = delay;
var P = 'p.n';
var j;
n + = 7;
while (i> 0) // Update HTML
p.innerHTML = P;
j = delay / i;
i - = 1 / delay;
let index;
let iIsOdd = (i% 2! = 0);
if (iIsOdd) let magic = (i% 2 * j - j + n / delay ^ j);
let magicIsOdd = (magic% 2! = 0); // 1
if (magicIsOdd) index = 1;
> Else index = 0;
>
> Else index = 2;
>
var n = setInterval (draw, delay);
Я розібрався з оператором var n = setInterval (draw, delay) ;. Метод setInterval повертає цілі числа, починаючи з одиниці, збільшуючи значення при кожному виклику. Це ціле число може використовуватися для clearInterval (тобто для скасування). У нашому випадку setInterval викликається всього один раз, а змінна n просто встановилася в значення 1.
Я також перейменував delay в DELAY для нагадування, що це всього лише константа.
І останнє, але не менш важливе, я помістив круглі дужки в i% 2 * j - j + n / DELAY ^ j для вказівки, що у ^ (побітового XOR) менший пріоритет, ніж в операторів%, *, -, + і /. Іншими словами, спочатку виконаються всі вищезгадані обчислення, а вже потім ^. Тобто виходить (i% 2 * j - j + n / DELAY) ^ j).
Уточнення: Мені вказали, що я помилково помістив p.innerHTML = P; // Update HTML в цикл, так що я прибрав його звідти.
const DELAY = 64; // approximately 15 frames per second 15 frames per second * 64 seconds = 960 frames
var n = 1;
var p = document.getElementById ( «p»);
// var draw = «for (n + = 7, i = delay, P = 'p. \ N'; i- = 1 / delay; P + = P [i% 2? (I% 2 * j-j + n /delay^j)1:2])j=delay/i;p.innerHTML=P »;
/ **
* Draws a picture
* 128 chars by 32 chars = total 4096 chars
* /
var draw = function () var i = DELAY; // 64
var P = 'p.n'; // First line, reference for chars to use
var j;
j = DELAY / i;
i - = 1 / DELAY;
let index;
let iIsOdd = (i% 2! = 0);
if (iIsOdd) let magic = ((i% 2 * j - j + n / DELAY) ^ j); // <——————
let magicIsOdd = (magic% 2! = 0); // 1
if (magicIsOdd) index = 1;
> Else index = 0;
>
> Else index = 2;
>
setInterval (draw, 64);
Остаточний результат виконання можна побачити тут.
Частина 2. Розуміння коду
Так що тут відбувається? Давайте розберемося.
Спочатку значення i встановлено на 64 за допомогою var i = DELAY ;, а потім кожен цикл воно зменшується на 1/64 (0,015625) через i - = 1 / DELAY ;. Цикл триває, поки i більше нуля (код while (i> 0)
Зображення складається з 32 рядків, з 128 символами в кожній. Дуже зручно, що 64 × 64 = 32 × 128 = 4096. Значення i може бути парним (НЕ непарним let iIsOdd = (i% 2! = 0);), якщо i є строго парним числом. Таке відбудеться 32 рази, коли воно дорівнює 64, 62, 60 і т. Д. Ці 32 рази index прийме значення 2 index = 2 ;, а до рядка додасться символ нового рядка: P + = «n»; // aka P [2]. Решта 127 символів в рядку приймуть значення p або.
Але коли встановлювати p, а коли.
Ну, для початку нам точно відомо, що слід встановити. при непарному значенні let magic = ((i% 2 * j - j + n / DELAY) ^ j) ;, або встановити p, якщо «магія» парна.
var P = 'p.n';
if (magicIsOdd) index = 1; // second char in P -.
> Else index = 0; // first char in P - p
>
Але коли magic парне, а коли непарне? Це питання на мільйон доларів. Перед тим як перейти до нього, давайте визначимо ще дещо.
Якщо прибрати + n / DELAY з let magic = ((i% 2 * j - j + n / DELAY) ^ j) ;, то вийде статична картинка, на якій взагалі нічого не рухається:

Тепер подивимося на magic без + n / DELAY. Як вийшла ця красива картинка?
(I% 2 * j - j) ^ j
Зверніть увагу, що виходить в кожному циклі:
j = DELAY / i;
i - = 1 / DELAY;
Іншими словами, ми може висловити j через кінцеве i як j = DELAY / (i + 1 / DELAY). Але оскільки 1 / DELAY занадто мале число, то для цього прикладу можна відкинути + 1 / DELAY і спростити вираз до j = DELAY / i = 64 / i.
У такому випадку ми можемо переписати (i% 2 * j - j) ^ j як i% 2 * 64 / i - 64 / i) ^ 64 / i.
Використовуємо онлайновий графічний калькулятор для відтворення графіків деяких з цих функцій.
Перш за все, отрісуем i% 2.
Виходить симпатичний графік зі значеннями y від 0 до 2.
Якщо отрисовать 64 / i, то отримаємо такий графік:
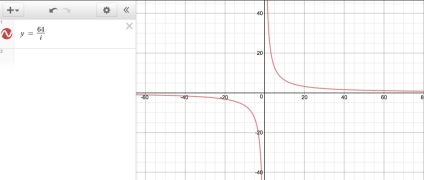
Якщо отрисовать всю ліву сторону вираження, то вийде графік, який виглядає як поєднання двох попередніх.
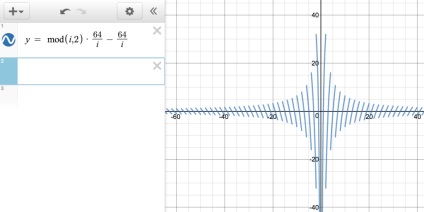
Зрештою, якщо ми отрісуем дві функції поруч один з одним, то побачимо наступне.
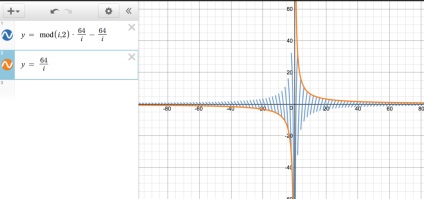
Про що говорять ці графіки?
Давайте пригадаємо питання, на який ми намагаємося відповісти, тобто яким чином вийшла така гарна статична картинка:

Ми знаємо, що якщо «магія» (i% 2 * j - j) ^ j приймає парне значення, то потрібно додати p, а для непарного числа потрібно додати.
Збільшимо перші 16 рядків нашого графіка, де i має значення від 64 до 32.

Він поверне 0, якщо обидва біти рівні 1 або обидва рівні 0.
Наша j починається з одиниці і повільно просувається до двійці, зупиняючись прямо біля неї, так що можемо вважати її завжди одиницею при округленні в меншу сторону (Math.floor (1.9999) === 1), і нам потрібна ще одна одиниця з лівого боку , щоб отримати в результаті нуль і дати нам p.
Іншими словами, кожна зелена діагональ є один ряд в нашому графіку. Оскільки для перших 16 рядів значення j завжди більше 1, але менше 2, то ми можемо отримати непарне значення тільки в тому випадку, якщо ліва сторона вираження (i% 2 * j - j) ^ j, вона ж i% 2 * i / 64 - i / 64, тобто зелена діагональ, теж буде вище 1 або нижче -1.
1 ^ 1 // 0 - even p
1.1 ^ 1.1 // 0 - even p
0.9 ^ 1 // 1 - odd.
0 ^ 1 // 1 - odd.
-1 ^ 1 // -2 - even p
-1.1 ^ 1.1 // -2 - even p
Якщо подивитися на наш графік, то там найправіша діагональна лінія ледь виходить вище 1 і нижче -1 (мало парних чисел - мало символів p). Наступна виходить трохи далі за ці межі, третя - ще трохи далі і т. Д. Лінія номер 16 ледь утримується в межах між 2 і -2. Після лінії 16 ми бачимо, що наш статичний графік змінює свій характер.
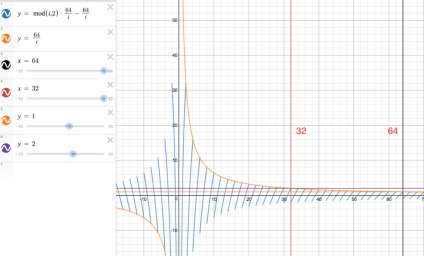
Після 16-го рядка значення j перетинає ліміт 2, так що змінюється очікуваний результат. Тепер ми отримаємо парне число, якщо зелена діагональна лінія вище 2 або нижче -2, або всередині рамок 1 і -1, але не стикається з ними. Ось чому ми бачимо на зображенні дві або більше груп символів p починаючи з 17-го рядка.
Якщо придивитися до кількох самим нижнім лініях в анімованої зображенні, то ви помітите, що вони не слідують одному і тому ж шаблону через велику флуктуації графіка.
Тепер повернемося до + n / DELAY. У коді ми бачимо, що значення n починається з 8 (1 від setInteval і плюс 7 на кожен виклик методу). Потім воно збільшується на 7 при кожному спрацьовуванні setInteval.
Після досягнення значення 64 графік внести такі зміни.
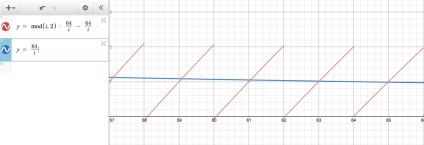
Зверніть увагу, що j як і раніше знаходиться близько одиниці, але тепер ліва половина червоної діагоналі в межах приблизно 62-63 знаходиться приблизно близько нуля, а права половина в межах приблизно 63-64 - близько одиниці. Оскільки наші символи з'являються в порядку спадання від 64 до 62, то можна очікувати, що права половина діагоналі в районі 63-64 (1 ^ 1 = 0 // even) додасть купку символів p, а ліва половина діагоналі в районі 62-63 ( 1 ^ 0 = 1 // odd) додасть купку точок. Все це буде наростати зліва направо, як звичайний текст.

До цього моменту кількість символів p зросла до постійної величини. Наприклад, в першому ряду половина всіх значень завжди будуть парними. Тепер символи p і. будуть тільки мінятися місцями.
Для прикладу, коли n збільшується на 7 на наступному виклику setInterval, графік трохи зміниться.
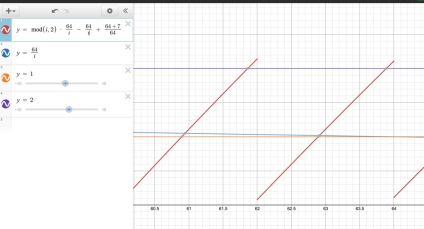
Зверніть увагу, що діагональ для першого ряду (близько позначки 64) зрушила приблизно на один маленький квадратик вгору. Оскільки чотири великих квадратів є 128 символів, в одному великому квадраті буде 32 символу, а в одному маленькому квадраті 32/5 = 6,4 сиволов (приблизно). Якщо подивимося на рендеринг HTML, то там перший ряд дійсно зрушився вправо на 7 символів.

І один останній приклад. Ось що відбувається, якщо викликати setInterval ще сім разів, а n буде дорівнювати 64 + 9 × 7.
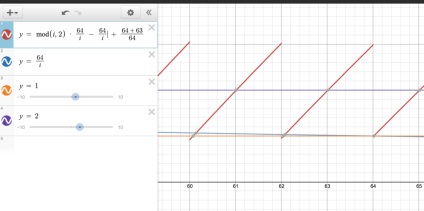
Для першого ряду j як і раніше дорівнює 1. Тепер верхня половина червоної діагоналі біля позначки 64 приблизно впирається в два, а нижній кінець близько одиниці. Це перевертає картинку в іншу сторону, оскільки тепер 1 ^ 2 = 3 // odd -. і 1 ^ 1 = 0 // even - p. Так що можна очікувати купу точок, за якими підуть символи p.
Виглядати це буде так.

Графік нескінченно зациклений.
Сподіваюся, наша робота має якийсь сенс. Навряд чи я коли-небудь зміг би самостійно придумати щось подібне, але було цікаво розібратися в цьому коді.