До сих пір ми обговорювали алгоритм навчання, в якому для кожного вхідного вектора активувався лише один нейрон Кохонена. Це називається методом акредитації. Його точність обмежена, так як вихід повністю є функцією лише одного нейрона Кохонена.
У методеінтерполяціі ціла група нейронів Кохонена, що мають найбільші виходи, може передавати свої вихідні сигнали в шар Гроссберга. Число нейронів в такій групі має вибиратися в залежності від завдання, і переконливих даних щодо оптимального розміру групи немає. Як тільки група визначена, її безліч виходів NETрассматрівается як вектор, довжина якого нормалізується на одиницю розподілом кожного значення NETна корінь квадратний з суми квадратів значень NETв групі. Всі нейрони поза групою мають нульові виходи.
Метод інтерполяції здатний встановлювати більш складні відповідності і може давати більш точні результати. Як і раніше, проте, немає переконливих даних, що дозволяють порівняти режими інтерполяції і акредитації.
Статистичні властивості навченої мережі
Метод навчання Кохонена володіє корисною і цікавою здатністю витягувати статистичні властивості з множини вхідних даних. Як показано Кохоненом [8], для повністю навченої мережі ймовірність того, що випадково обраний вхідний вектор (відповідно до функцією щільності ймовірності вхідного безлічі) буде найближчим до будь-якого заданого вагового вектора, дорівнює 1 / k, де k - число нейронів Кохонена. Це є оптимальним розподілом ваг на гіперсфері. (Передбачається, що використовуються всі вагові вектори, що має місце лише в тому випадку, якщо використовується один з обговорюваних методів розподілу ваг.)
Навчання шару Гросберга
Шар Гроссберга навчається відносно просто. Вхідний вектор, який є виходом прошарку Кохонена, подається на шар нейронів Гроссберга, і виходи шару Гроссберга обчислюються, як при нормальному функціонуванні. Далі, любий каприз коригується лише в тому випадку, якщо він з'єднаний з нейроном Кохонена, що має ненульовий вихід. Величина корекції ваги пропорційна різниці між вагою і необхідним виходом нейрона Гроссберга, з яким він з'єднаний. У символьній записи
де ki - виходi- го нейрона Кохонена (тільки для одного нейрона Кохонена він відмінний від нуля); уj -j -а компонента вектора бажаних виходів.
Спочатку берется рівним
0,1 і потім поступово зменшується в процесі навчання.
Звідси видно, що ваги шару Гроссберга будуть сходитися до середніх величин від бажаних виходів, тоді як ваги шару Кохонена навчаються на середніх значеннях входів. Навчання шару Гроссберга - це навчання з учителем, алгоритм має бажаним виходом, за яким він навчається. Навчається без учителя, самоорганізується шар Кохонена дає виходи в недетермінірованних позиціях. Вони відображаються в бажані виходи шаром Гроссберга.
Мережа зустрічного поширення повністю
На рис. 4.4 показана мережа зустрічного поширення цілком. В режимі нормального функціонування пред'являються вхідні вектори Х і Y, і навчена мережа дає на виході векториX 'іY'. є апроксимаціями відповідно дляХ іY. Вектор іY передбачаються тут нормалізованими одиничними векторами, отже, породжувані на виході вектори також матимуть тенденцію бути нормалізованими.
В процесі навчання вектори Х іY подаються одночасно і як вхідні вектори мережі, і як бажані вихідні сигнали. ВекторХ використовується для навчання виходовX '. а вектор Y - для навчання виходів Y 'шару Гроссберга. Мережа зустрічного поширення цілком навчається з використанням того ж самого методу, який описувався для мережі прямої дії. Нейрони Кохонена приймають вхідні сигнали як від векторовX. так і від векторовY. Але це не відрізняються від ситуації, коли є один великий вектор, складений з векторовХ іY. і не впливає на алгоритм навчання.
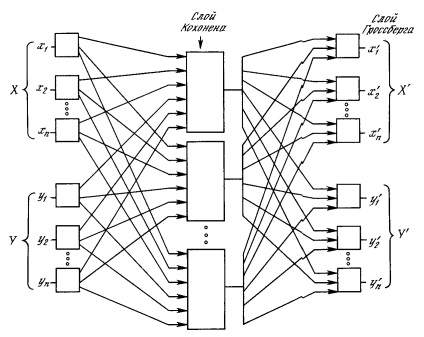
Мал. 4.4. Повна мережа зустрічного поширення
В як результуючий виходить одиничне відображення, при якому пред'явлення пари вхідних векторів породжує їх копії на виході. Це не представляється особливо цікавим, якщо не помітити, що пред'явлення тільки вектора Х (з векторомY. Рівним нулю) породжує як виходиX '. так і виходи Y '. ЕсліF- функція, отображающаяХ Вy '. то мережу аппроксимирует її. Також, есліF оборотна, то пред'явлення тільки вектораY (прирівнюється нулю) порождаетX '. Унікальна здатність породжувати функцію і зворотну до неї робить мережу зустрічного поширення корисної в ряді програм.
Мал. 4.4 на відміну від первісної конфігурації [5] не демонструє протитечія в мережі, за яким вона отримала свою назву. Така форма обрана тому, що вона також ілюструє мережу без зворотних зв'язків і дозволяє узагальнити поняття, розвинені в попередніх розділах.