1.4.3 Римська нумерація
Стародавні римляни користувалися нумерацією, яка зберігається до теперішнього часу під ім'ям «римської нумерації». Ми користуємося їй для позначення століть, ювілейних дат, найменування з'їздів і конференцій, для нумерації розділів книги або строф вірша.
У пізнішому своєму вигляді римські цифри виглядають так:,,,,,,.
У римській нумерації виразно позначаються сліди п'ятиричної системи числення. У мові ж римлян (латинською) ніяких слідів п'ятиричної системи немає. Значить, ці цифри були запозичені римлянами у іншого народу (імовірно у етрусків).
Всі цілі числа (до 5000) записуються за допомогою повторення вищенаведених цифр. При цьому, якщо велика цифра стоїть перед меншою, то вони складаються, якщо ж менша стоїть перед більшою (в цьому випадку вона не може повторюватися), то менша віднімається з більшою. Поспіль одна і та ж цифра ставиться не більше трьох разів. Розглянемо приклади.
Приклад 1.4 Запис чисел римськими цифрами
Виконання арифметичних дій над багатозначними числами в цьому записі дуже громіздко і важко. Проте римська нумерація переважала в Італії до XIII століття, а в інших країнах Західної Європи - до XVI століття.
1.4.4 Вавилонська помісна нумерація
У стародавньому Вавилоні приблизно за 40 століть до нашого часу створилася помісна (позиційна) нумерація, тобто такий спосіб зображення чисел, при якому одна і та ж цифра може позначати різні числа, залежно від місця, займаного цією цифрою. Наша теперішня нумерація - теж помісна, проте в вавилонській помісної нумерації ту роль, яку відіграє у нас число 10, грало число 60, і тому цю нумерацію називають шестидесяткова. Числа, менші 60, позначалися за допомогою двох знаків: для одиниці і для десятка. Вони мали клиноподібний вигляд, так як вавилоняни писали на глиняних дощечках паличками трикутної форми. Ці знаки повторювалися потрібне число раз. При відсутності проміжного розряду застосовувався знак. Запис чисел до 60 показана в прикладі 1.5. Спосіб позначення чисел, великих 60 зведений в таблицю 1.3.
Приклад 1.5 Запис вавилонської клинописом чисел до 60
Шестидесяткова запис цілих чисел не набула поширення за межами ассиро-вавилонської царства, але шестідесятірічних дробу проникли далеко за ці межі: в країни Середнього Сходу, Середньої Азії, в Північну Африку і Західну Європу. Вони широко застосовувалися, особливо в астрономії, аж до винаходу десяткових дробів. Сліди шестідесятірічних дробів зберігаються і понині в розподілі кутового і дугового градуса (а також години) на 60 хвилин і хвилини на 60 секунд.
Інформація про роботу «Системи числення»
Розділ: Цифрові пристрої
Кількість знаків з пробілами: 95849
Кількість таблиць: 35
Кількість зображень: 321
Схожі роботи

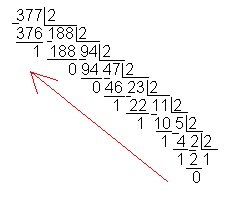
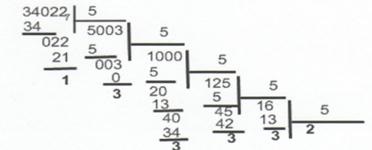
множити на основу нової системи числення до тих пір, поки в новій дріб не може бути потрібної кількості цифр, яке визначається необхідною точністю уявлення дробу. Правильна дріб в новій системі числення записується з цілих частин творів виходять при послідовному збільшенні, причому перша ціла частина буде старшої цифрою нової дробу. Розглянемо як приклад.
подання до них досить великих чисел, так як при цьому виходить надзвичайно громіздка запис чисел або потрібно дуже великий алфавіт використовуваних цифр. У ЕОМ застосовують тільки позиційні системи числення, в яких кількісний еквівалент кожної цифри алфавіту залежить не тільки від виду цієї цифри, але і від її місця розташування в запису числа. Позиційні системи числення В.


послідовності 0 та 1. Наприклад ціле невід'ємне число А2 = Т 111100002 буде зберігатися в осередку наступним чином: 1 1 1 1 0 0 0 0 Значить, ми можемо записати все числа від 0 до 255 в двійковій системі числення в 1 комірці пам'яті. 2.2 Подання чисел в комп'ютері Цілі числа в комп'ютері зберігаються в комірках пам'яті, в цьому випадку кожному розряду комірки пам'яті відповідає.
народження (рік, число, місяць). 4. Підведення підсумків. Домашнє завдання. Вчити записи в зошитах. Висновок У цій роботі було розглянуто роль і місце елективних курсів в передпрофільне навчання, а також розроблений елективний курс не тему «система числення» в передпрофільне навчання інформатиці. У першій частині роботи були виявлені головні особливості предпрофильной п