Онлайн калькулятор на нашому сайті легко і швидко вирішує тригонометричні функції. вам не знадобиться таблиця тригонометричних функцій. З нашим калькулятором можна назавжди забути, що таке таблиця Брадіса! Наш безкоштовний калькулятор дозволяє вирішувати і найпростіші завдання (наприклад, знайти косинус або синус кута), і складні вирази з використанням зворотних і гіперболічних функцій тригонометрії.
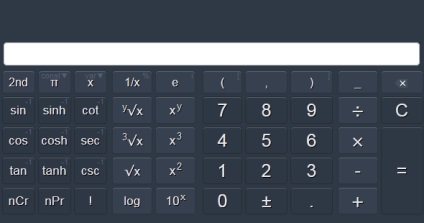
Кнопки калькулятора для вирішення тригонометричних функцій:
Наш тригонометричний калькулятор може здійснювати обчислення як в градусах, так і в радіанах. Таким чином, знайти косинус кута можна незалежно від одиниці виміру, в якій він заданий. Це дуже зручно і економить масу часу при ємних розрахунках. Перш ніж приступити до обчислень, потрібно на панелі управління вказати, яка одиниця вимірювання кутів буде використовуватися: градуси (Deg) або радіани (Rad).
Вибір одиниці виміру кута:
Зверніть увагу, що в одній операції не можна використовувати різні одиниці вимірювання кутів, іншими словами вираз «сума синус 30 градусів і косинус пі =» - буде пораховано невірно!
Нижче перераховані способи рішень різних тригонометричних функцій в нашому онлайн калькуляторі.
Прості тригонометричні функції
Прості тригонометричні функції: синус - sin (α), косинус - cos (β) і тангенс - tan (y). Поруч вказані їх позначення так, як вони використовуються в калькуляторі (в зарубіжній літературі тангенс скорочено позначається tan, в російській - tg).
Кнопки калькулятора, що відповідають за прості тригонометричні функції:
Функція косинуса є парною, тому її значення для негативного кута буде позитивним. Синус, тангенс і котангенс - непарні тригонометричні функції, відповідно, значення тригонометричних функції для негативних кутів також будуть негативними. Онлайн калькулятор сам враховує парність тригонометричних функцій при множенні і діленні. Вам не буде потрібно постійно звертати увагу на дотримання правила знаків.
Приклад обчислень з простими тригонометричними функціями:
Зворотні тригонометричні функції
Зворотні тригонометричні функції: арксинус - asin (), арккосинус - acos () і арктангенс - atan ().
Кнопки калькулятора, що відповідають за зворотні тригонометричні функції:
Якщо не вдаватися в формули і подробиці щодо одиничному колі, то зворотні тригонометричні функції можна пояснити на простому прикладі: арккосинус x - це кут, косинус якого дорівнює x. Зворотні тригонометричні функції є багатозначними, і одного значення аргументу належить безліч значень самої функції.
Приклад вираження зі зворотними тригонометричними функціями:
гіперболічні функції
Гіперболічні функції: гіперболічний синус - sinh (), гіперболічний косинус - cosh () і гіперболічний тангенс tanh (). Гіперболічні (кругові) функції - сімейство елементарних тригонометричних функцій, виражених через експоненту.
Кнопки калькулятора, що відповідають за гіперболічні функції:
Приклад рішення гіперболічної функції:
Зворотні гіперболічні функції: гіперболічний арксинус - asinh (), гіперболічний арккосинус - acosh () і гіперболічний арктангенс - atanh ().
Кнопки калькулятора, що відповідають за зворотні гіперболічні функції:
Приклад розв'язання оберненої гіперболічної функції:
Всі функції нашого безкоштовного калькулятора зібрані в одному розділі. Функції онлайн калькулятора >>