Наведені нижче текст є частиною книги «Перший крок в квантову реальність».
4. Узагальнення тригонометричних функцій на випадок будь-яких кутів.
Переконайтеся самостійно, що все, сказане вище про тригонометричні функції, справедливо для ситуації, зображеної на малюнку:
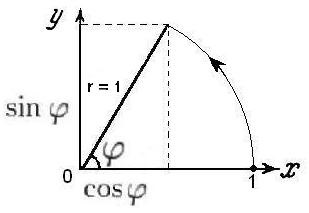
- вершина кута φ прямокутного трикутника поєднана з початком координат,
- гіпотенуза трикутника, що є також і радіусом окружності, дорівнює одиниці, r = 1,
- косинус є проекцією радіуса на вісь абсцис,
- синус є проекцією радіуса на вісь ординат.
Все це правильно, але поки тільки для гострих кутів, коли радіус-гіпотенуза знаходиться в першій чверті.
Узагальнення ситуації на випадок будь-яких кутів очевидним чином випливає з малюнка:
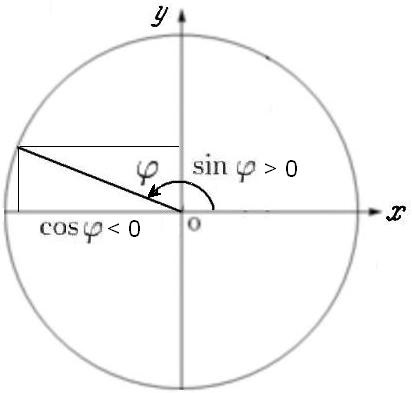
А саме, для будь-яких кутів косинус, - проекція одиничного радіуса на вісь абсцис (O x), синус - проекція одиничного радіуса на вісь ординат (O y), причому в тих випадках, коли проекція потрапляє в негативну область координатних осей, функцій приписується знак мінус.
Всі інші тригонометричні функції виражаються через синус і косинус, відповідні формули наведені вище.
Найбільш важливі властивості і графіки тригонометричних функцій
Функція f (x) називається парною, якщо f (- x) = f (x), і непарної, якщо f (- x) = -f (x).
Графік парної функції симетричний щодо осі ординат (O y), а графік непарної функції симетричний відносно початку координат. З графіків видно, що косинус є парною функцією, а синус, тангенс і котангенс - непарні.
Більшість функцій не є ні парними, ні непарними, вони є сумою двох доданків:
Перший доданок - парна частина, другий доданок - непарна частина.
Але основні тригонометричні функції мають, як ми тепер переконалися, цілком певну парність.
5. Що обов'язково потрібно пам'ятати про тригонометричні функції.
Перш за все - узагальнена визначення синуса і косинуса.
Звідси відразу ж випливає, що, наприклад, косинус в четвертій чверті позитивний, а синус негативний, або синус 180 ° дорівнює нулю, а косинус дорівнює мінус одиниці. І т.п.
Корисно також вміти малювати графіки синуса, косинуса, тангенса і котангенс з обов'язковим зазначенням значень на осях абсцис і ординат, так, як це показано на малюнках, наведених у таблиці.
Ще дуже важливі формули:
Останні дві формули можна легко відновити з рівності:
Крім того, корисно пам'ятати про парності-непарності тригонометричних функцій і знати їх періоди.
Корисні також формули приведення, які дозволяють виразити значення тригонометричних функцій для будь-яких кутів через значення тригонометричних функцій кутів першої чверті.
Щоб уникнути необхідності користуватися подібними розрахунками, застосовують мнемонічне правило:
1. Якщо обчислюється тригонометричні функції кутів 90 ° ± α або 270 ° ± α. то синус змінюється на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс. У разі кутів 180 ° ± α або 360 ° ± α функції залишаються незмінними, тобто синус залишається синусом і т.п.
2. Знак результату такої ж, як у вихідної функції в тій чверті, в яку потрапляє вихідний кут.
Наприклад: cos (180 ° - α) = - cos α.
Косинус залишається косинусом, тому що 180 °, а не 90 ° або 270 °.
Вихідний кут (180 ° - α) у другій чверті, де косинус, початкова функція, негативна, тому знак мінус.
Ось, мабуть, і все!
Подивіться, скільки всяких тригонометричних формул в довіднику! Але майже всі основні формули легко виходять за одне-два дії з тих співвідношень, які ми розглянули.
Тому найпростіше тригонометричні формули не заучувати, а виводити в міру необхідності.
Звичайно, не завадило б знати тригонометрію краще, але тут наведено необхідний мінімум. Якщо при подальшому читанні щось знадобиться додатково, то будуть дані необхідні роз'яснення.