Цех кондитерської фабрики виробляє три асортиментні групи цукерок, умовно позначені М1. М2. М3 / в од. /.
Для їх виробництва використовуються основні види ресурсів / сировини / трьох видів, умовно названих П1. П2. П3 / в од. /.
Витрата кожного ресурсу на виробництво одиниці продукції є за-даної величиною, визначається за рецептурою і позначається символами А11. a12. А33. де а - норма витрати, перша підрядкові 1 - номер ресурсу, друга підрядкові 1, 2, 3 - номер асортиментної групи цукерок.
Наявність кожного ресурсу для виробництва всіх, груп цукерок приймає-ся як відома величина і позначається символами в1. в 2. у 3 .
Прибуток на продукцію також приймається як відома величина і обо-значущих символів c1. c2. с3.
Перераховані параметри є величинами відомими і висловлюють-ся в єдиних одиницях виміру, крім прибутку. Прибуток або інший який показник, який є критерієм оптимальності, виражається в одиницях через виміри доходу / наприклад, прибутку /, одержуваного від виробництва одиниці продукції в грошовому або іншому якомусь виразі.
Оскільки рішення задачі полягає в пошуку такого плану виробництва, який забезпечував би в прийнятих умовах найбільший дохід, приймається-ються ті величини, які є невідомими і позначають кількісних-ва кожної групи цукерок, що включаються до плану виробництва: x1 для M1; х2 для М2; х3 для М3.
Економіко-математична модель в символічному вигляді.
Умови невід'ємності невідомих х1 ≥ 0, х2 ≥ 0, х3 ≥ 0
Символічна модель, наповнена чисельної інформацією, буде мати наступний вигляд:
Прибуток від реалізації продукції, що випускається повинна бути максимальною-ної, тобто F = 20х1 + 24х2 + 28х3 = max;
Для вирішення завдання симплексним методом нерівності перетворюються в еквівалентні рівності шляхом додавання в кожне нерівність по одному до-виконавчими невідомому з коефіцієнтом + 1 і нульовим рівнянням при-були. Для зручності розрахунків ліві і праві частини рівнянь змінюються місця-ми. У цьому випадку вихідні нерівності візьмуть вид симплексних рівнянь:
Коефіцієнти при невідомих записуються в симплексній таблиці, в якій виконуються розрахунки і відображаються отримані результати.
Потім елементи стовпця Х0 (вільні величини) ділять на відповідаю-щие коефіцієнти ключового стовпця і отримані результати зіставляють між собою. Рядок з найменшим відношенням приймається за ключову і також для зручності виділяється. У нашому випадку 266/3 = 88,7; 200/4 = 50; 303/1 = 303. Найменше ставлення 50 має терміну х5. вона і буде ключовою. Ключовий елемент 4.
Далі елементи таблиці перетворюються і записуються в нову таблицю. Спочатку перетворять елементи ключовий рядки шляхом ділення їх на ключовий елемент. Перетворені елементи записують в тому ж самому місці.
У стовпчиках Ро і Cj займають місце вводиться в план невідома х3 з при-бувальщиною 28 (ітерація 1-я). Інші елементи перетворюються за наступним правилом:
- для перетворюється елемента в його стовпці знаходять елемент ключовий рядки, а в його рядку - елемент ключового стовпця;
- відповідні елементи ключовий рядки і ключового стовпця пере-які множаться і отриманий добуток ділять на ключовий момент;
- частка від ділення вираховують із значення елемента, яке він мав до перетворення, і отриманий результат буде перетворений елементом, ко-торий записується в нову таблицю в тому ж самому місці. Слідуючи цьому пра-вилу, перетворення елементів стовпця х0 буде:
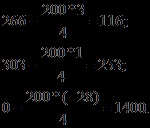
Включення на першій ітерації в план невідомої х3 забезпечить суму прибутку 1400 руб.
Рішення завдання триває, так як в цільової рядку два отрицатель-них елемента. Найбільший по модулю елемент -13. Він знаходиться в стовпці х1. який приймається за ключовою, а ключовий рядком буде х6 (116: 1,3 = 92,8; 50: 0,3 = 200; 253: 2,8 = 92), ключовим елементом 2,8. Елементи таблиці перетворень-ються в тому ж порядку по викладеному правилом і записуються в нову таб-лиця.
В останній таблиці цільовий рядок має тільки позитивні елементів-ти. Це означає, що складений план оптимальний і подальше поліпшення його неможливо.
Як видно з таблиці, оптимальний план передбачає випуск про-дукції П1 27 од. (Х1 = 27), П3 92 од. (Х3 = 92), додаткового невідомого П4 1 од. (Х4 = 1). П2 і додаткові невідомі в план не увійшли, отже, х2 = 0, х5 = 0 х6 = 0. Підставивши значення невідомих в рівняння, отримаємо:
2 * 92 + 4 * 0 + 3 * 27 + 1 = 266
1 * 92 + 3 * 0 + 4 * 27 + 0 = 200
3 * 92 + 2 * 0 + 1 * 27 + 0 = 303
F = 20 * 92 + 24 * 0 + 27 * 28 = 2596
Аналіз оптимального плану.
а) Запаси сировини трьох видів використовуються не повністю, так як х4 = 1, а х5 = х6 = 0.
б) Розглянемо елементи матриці.
Від випуску продукції II слід відмовитися.
Елементи стовпчика х5 показують, що збільшення запасів цукру на I од. (Х5 = 1) дозволить збільшити випуск продукції III виду на 0,3 од. Сума прибутку збільшиться на 5,8 руб.
Елементи стовпчика х6 показують, що збільшення запасів жиру на I од. (Х6 = 1) дозволить зменшити випуск тільки продукції III виду на 0,1 од. (27 - 0.1) Сума при-були збільшиться на 4,7 руб.
Зниження запасів сировини призводить до змін випуску продукції і суми прибутку в зворотному порядку.
Елементи цільової рядки оптимального плану називаються подвійними оцінками, які визначають величину зміни прибутку при зміні за-пасів сировини на I од.
Потрібно визначити мінімальну за вартістю суміш сировини для виготов-лення харчових концентратів, які повинні містити живильні ве-щества (П). Ці речовини містяться в сировині (М) в різних поєднаннях. З-тримання поживних речовин у сировині та готовому продукті, а також ціна на ка-ждий вид сировини показані в таблиці.
Елементи цільової рядки розраховують за звичайними правилами і отримай-ють негативні знаки.
На відміну від обчислювальної процедури основного симплексного методу рішення задач двоїстим методом виконується в зворотному порядку.
У підсумковому стовпці вільні числа мають негативні знаки. Це яв-ляется свідченням того, що даний план не можна вважати допустимим, оскільки він суперечить економічному глузду. План можна вважати допустимим тільки тоді, коли в підсумковому стовпці негативно не чисел.
Ліквідація негативних чисел в підсумковому стовпці починається з най-більшого по абсолютній величині. У нашому прикладі таким числом є (-140). Рядок х5. в якій знаходиться це число, приймається за ключову і со-відповідально виділяється.
Визначивши ключовий рядок, знаходимо ключовий стовпець. Для цього потрібно елементи цільової рядки розділити на елементи ключовий рядки і з отриманий-них відносин вибрати найменше. Стовпець, який має найменшу ставлення-ня, приймається за ключовою і так само як ключова рядок, виділяється.
Стовпці х1. х2. х3 матимуть такі відно-шення:
Найменший стосунок має стовпець х1, він і буде ключовим.
Визначивши ключовий рядок, ключовий стовпець і ключове число, за звичайними правилами перетворюються всі елементи матриці і записуються в но-вої таблиці.
Рішення завдання починається з розподілу у наявних у постачальників обсягів вивезення між споживачами з урахуванням обсягів завезення. Для початкового розподілу застосовуються методи: північно-західного кута, найменшого елемента по рядку, найменшого елемента по стовпцю, найменшого елемента матриці.
Спосіб північно-західного кута полягає в тому, що розбраті-поділ обсягів вивезення проводиться, починаючи з верхнього ліво-го кута таблиці і закінчуючи нижнім кутом її. Результати распреде-лення показані в таблиці.
Постачальники і обсяги вивезення, т
Споживачі і обсяги завезення
Перевірка плану на оптимальність. Коли вихідний план отримано і розрахована відповідна йому сумарна тонно-кілометрова робота, визначають, чи є цей план оптимальним. Для перевірки плану на оптимальність застосовується метод потенціалів.
Суть методу потенціалів полягає в тому, що для кож-дою рядки і кожного стовпця таблиці (матриці) визначають спе-ціальні числа, звані потенціалами. За допомогою цих потен-циал можна встановити, чи потрібно заповнювати вільну клітину матриці або її потрібно залишити незаповненою.
Для вирішення завдань методом потенціалів вихідний план дол-дружин мати кількість заповнених клітин m + n - 1 (m - число рядків, n - число стовпців). Якщо план не відповідає цим вимогам, то не для всіх рядків і стовпців можна рассчи-тать потенціали, а без них не можна перевірити план на оптималь-ність.
Потенціали рядків і стовпців визначаються по заповненим клітинам, які знаходяться на їх перетині.
Елемент заповненої клітини повинен дорівнювати сумі потен-циал рядки і стовпці, на перетині яких знаходиться ця заповнена клітина.
Для початку обчислень перший потенціал для рядків або стовпчиків приймається умовно рівним нулю, всі інші потенціали визначаються за допомогою елементів заповнених клітин.
Позначивши потенціали рядків ui. потенціали стовпців Vj, елементи заповнення клітин
, можна записати порядок розрахунку потенціалів для загального випадку.
З основного вимоги
= Ui + Vj випливає:
З цих виразів видно, що для розрахунку потенціалу рядки необхідно мати заповнену клітку, в стовпці якої потенціал вже визначено, а для розрахунку потенціалу стовпчика потрібна заповнена клітина, що має потенціал в рядку.
Потенціали показані в таблиці.
Після того, як по рядках і стовпцях визначені потенциа-ли, з їх допомогою з'ясовується, чи є план оптимальним, і якщо немає, то як його можна поліпшити. З цією метою для кожної вільної клітини обчислюється сума потенціалів рядків і стовпців, на перетині яких знаходиться ця клітина.
Порівняння суми потенціалів з величиною елемента в свобод-них клітинах дозволяє визначити, чи потрібно заповнювати цю клітку або її потрібно залишити вільною.
При вирішенні завдань на мінімум функціоналу (в нашому випадку на мінімум тонно-кілометрової роботи) не заповнюються ті свобод-ні клітини, в яких сума потенціалів менше величини еле-мента (в нашому випадку - відстані).
Іншими словами, якщо характеристика, значення якої дорівнює різниці
- (Ui + Vj), позитивна, то вільна мет-ка не заповнюється при вирішенні задачі на мінімум функції.
Вільні клітини, що мають нульове значення характеристики, показують на те, що їх заповнення призведе до перерозподілу поставок, але обсяг робіт (значення функціоналу) залишиться неіз-менним.
Суми потенціалів, значення елементів та характеристики для незаповнених клітин наведені в таблиці.
У початковому плані шість клітин мають позитивні характеристики, в дев'яти клітинах характеристики негативні.
Так як завдання вирішується на мінімум цільової функції, то саме ці негативні клітини повинні бути заповнені постачальниками. Але заповнення вільної клітини і пов'язане з ним пере-розподіл поставок проводиться не ізольовано, а в зв'язку з декількома заповненими клітинами. Цей зв'язок виявляється шляхом побудови замкнутих багатокутників, вершинами яких є-ються клітини таблиці. Одна вершина багатокутника знаходиться в вільній клітці, а всі інші - в заповнених клітинах. Багатокутник, або як його називають ланцюг, має прямі кути і парне число вершин.
В результаті перерозподілу в кожній вершині (клітці) ланцюга відбувається зміна величини поставок: в одних клітинах вони збільшуються, в інших - зменшуються.
Ті клітини ланцюга, у яких поставки збільшуються, називаючи-ються позитивними, а ті, у яких поставки зменшуються - негативними. Кожна ланцюг має однакове число позитивними-них і негативних вершин (клітин). Позитивні і негативні-тільні вершини чергуються. Якщо вільну клітину, в яку передбачається зробити запис, прийняти як позитивну (оскільки зміна відбудеться в бік збільшення), то сле-дме клітина буде негативною, потім знову позитивної, знову негативною, і т.д.
З вільних клітин для заповнення вибирають зазвичай клітку, яка має найбільшу негативну характеристику. У неї записують саму найменшу величину з негативних вершин ланцюга.
+П4М1 -П1М1 + П1М2 -П2М2 + П2М4 -П3М4 + П3М5 -П4М5
Постачальники і обсяги вивезення, т
Споживачі і обсяги завезення
+П2М5 -П4М5 + П4М1 -П1М1 + П1М4 -П2М4
Постачальники і обсяги вивезення, т
Споживачі і обсяги завезення
+П2М5 -П4М5 + П4М1 -П1М1 + П1М4 -П2М4
Постачальники і обсяги вивезення, т
Споживачі і обсяги завезення
+П3М2 -П1М2 + П1М4 -П2М4 + П2М5 -П3М5
Постачальники і обсяги вивезення, т
Споживачі і обсяги завезення
+П4М3 -П2М3 + П2М5 -П4М5
Постачальники і обсяги вивезення, т
Споживачі і обсяги завезення
+П2М1 -П2М3 + П4М3 -П4М1
Постачальники і обсяги вивезення, т
Споживачі і обсяги завезення
+П2М2 -П2М5 + П3М5 -П3М2
Постачальники і обсяги вивезення, т
Споживачі і обсяги завезення
Всі вільні клітини мають позитивні характеристики, які свідчать про те, що подальше поліпшення плану неможливо і отриманий план є оптимальним.
Обсяг робіт складе: 32 * 30 + 112 * 15 + 76 * 9 + 52 * 24 + 20 * 27 + 76 * 21 + 16 * 11 + 80 * 27 + 36 * 8 = 9332 ткм.
Всі матеріали в розділі "Економіко-математичне моделювання"