
Урок супроводжується презентацією, що містить різні типи завдань на застосування графів: завдання вирішуються з кінця, що використовують арифметику залишків, завдання на відсотки, завдання, в яких заданий плоский граф потрібно викреслити, не відриваючи олівця від паперу і не обводячи двічі один і той же ділянку графа . У теоретичному матеріалі до уроку містяться поняття: граф, ребро графа, парні, непарні графи Урок містить етапи: усний рахунок, перевірка домащней роботи, гра-лічильник, домашнє завдання, підсумок уроку. Презентація містить історичний матеріал про Ейлера і красиві висловлювання.
Рішення задач за допомогою графів 5 клас.
закріпити поняття графа і відпрацювати навички використання графів для вирішення завдань;
перевірити рівень засвоєння поняття графа через вміння застосовувати набуті знання для вирішення нових завдань.
розвивати логічне і творче мислення учнів, кмітливість, спостережливість, інтуїцію і адекватність при оцінці роботи однокласника;
формувати активний пізнавальний інтерес до предмету.
виховувати повагу до історичних особистостей, любов до літератури на прикладі текстів підібраних завдань.
1. Організаційний момент
2. Перевірка домашнього завдання
"Життя прикрашається двома питаннями: заняттям математикою і її викладанням" Пуассон С.II.
Вивчення математики здійснюється в процесі вирішення завдань і вправ.
Хлопці, сьогодні на уроці ми будемо вирішувати завдання, пов'язані з графами, які вирішуються з кінця, що використовують арифметику залишків, завдання на відсотки.
Почнемо з домашнього завдання на відсотки
5 ∙ 0,35 = 1,75 літрів жиру в 5 літрах вершків
4 ∙ 0,20 = 0,8 літрів жиру в 4 літрах
1,75 + 0,8 = 2,55 літрів жиру в суміші
5 + 4 + 1 = 10 літрів суміш
5. 2,55: 10 = 0,255 літрів = 25,5% жирність суміші
Проведемо гру: "Кращий лічильник" (на оцінку).
Виберіть по 2 лічильника з кожного ряду.
Ще Песталоцці говорив: "Рахунок і обчислення - основа порядку в голові"
З'ясуємо - Хто з вас правильно відповість на більшу кількість запитань. Хлопці, допомагайте - вважайте правильні відповіді своїх хлопців.
1) Фізик, статут, ліг спати о 10 годині вечора; попередньо завів будильник на 12 годин наступного дня. Скільки годин він встиг проспати, перш ніж будильник його розбудить? [2]
4) Якою буде залишок від ділення твори на 6
67 = 1 (Мод 6) (Це завдання на арифметику залишків)
5) Знайди залишок від ділення на 5 чергові частини (7 + 56 + 558 + 5558) / 5
6) Вирішити ур - е: (((х + 2) / 4) -2) * 6 = 12 [14]
7) Знайди число, якщо 3% від нього 24 [800]
9) 3000% від 50 [1500]
10) Знайди процентне відношення чисел 48 до 16 [300%]
11) Розрахуйте 0.1% від 700 [0.7]
Перемогли всі, тому що всі брали участь разом з ними і перевіряли правильність відповідей.
4) Видатна жінка - математик Ковалевська підкреслювала: "У математиків
існує своя мова - це формули "
Завдання, які вирішуються з кінця
(Сценка) "Селянин і рис":
Йде селянин і бідкається: "ех! Життя моє гірка! Заїла потреба зовсім! Ось в кишені тільки кілька грошів мідних бовтається, та й ті зараз потрібно віддати. І як це у інших буває, що на всякі гроші вони ще гроші отримують? Право, хоч би хто допомогти мені захотів ".
Тільки встиг це сказати, як глядь, а перед ним рис варто.
-Що ж, - каже, - якщо хочеш, я тобі допоможу. І це зовсім неважко. Ось бачиш цей міст через річку?
-Бачу! - каже селянин, а сам зніяковів.
-Ну, так варто тобі перейти тільки через міст - у тебе буде вдвічі більше грошей, ніж є. Перейдеш тому, знову стане вдвічі більше, ніж було. І кожен раз, як ти будеш переходити міст, у тебе буде вдвічі більше грошей, ніж було до цього переходу.
-Та невже? - каже селянин.
-Вірне слово! - запевняє рис. - Тільки, цур, домовленість! За те, що я тобі подвоюю гроші, ти кожен раз, перейшовши через міст, віддавай мені по 24 копійки. Інакше не згоден.
-Ну, що ж, це не біда! - каже селянин. - Раз гроші все будуть подвоюватися, так чому ж 24 копійки тобі кожен раз не віддати? Ну-ка, спробуємо!
Перейшов він через міст один раз, порахував гроші. Дійсно, стало вдвічі більше. Кинув він 24 копійки межу і перейшов вдруге. Знову грошей стало вдвічі більше, ніж перед цим. Відрахував він 24 копійки, віддав межу і перейшов через міст в третій раз. Грошей стало знову вдвічі більше. Але тільки і виявилося їх рівно 24 копійки, які за домовленістю про мав віддати під три чорти. Віддав він їх і залишився без копійки.
Скільки ж у селянина було грошей спочатку?
1. ((х 2 - 24) 2 - 24) 2 - 24 = 0 х = 21
Якщо після останнього переходу у селянина виявилося 24, то до того було 12, до них додамо 24, (які він віддав) отримаємо 36 значить до другого переходу було 38 коп. До них додав 24 отримаємо 42, значить було 21 коп.
Прогадав селянин. Видно, що на чужій рада завжди треба ще свойуміметь.
5. Завдання на графи.
Теорія графів знаходить застосування, не тільки в математиці, але наприклад, в геоінформаційних системах (ГІС). Існуючі або знову проектовані будинки, споруди, квартали і т. П. Розглядаються як вершини, а що з'єднують їх дороги, інженерні мережі, лінії електропередач і т. П. - як ребра. Застосування різних обчислень, вироблених на такому графі, дозволяє, наприклад, знайти найкоротший об'їзний шлях або найближчий продуктовий магазин, спланувати оптимальний маршрут.
Перший тип завдань
«Хто грає Ляпкина-Тяпкіна?»
У шкільному драмгуртку вирішили ставити гоголівського «Ревізора». І тут розгорівся запеклу суперечку. Все почалося з Ляпкина-Тяпкіна. - Ляпкин-Тяпкін буду я! - рішуче заявив Гена.
- Ні, я буду Ляпкіних-Тяпкін, - заперечив Діма.
- З раннього дитинства мріяв втілити цей образ на сцені.
- Ну, добре, згоден поступитися роль, якщо мені дадуть зіграти Хлестакова, - проявив великодушність Гена.
-. А мені - Осипа, - не дав йому в довготерпінню Діма. - Хочу бути суниці або Городничим, - сказав Вова.
- Ні, городничим буду я, - хором закричали Алік і Боря. - Або Хлестакова, - додали вони одночасно.
Чи вдасться розподілити ролі так, щоб виконавці були задоволені? (Ми не запитуємо, чи будуть задоволені глядачі.)
Від кожного учасника проведемо відрізки, тобто ребра до ролей, яку він хотів би зіграти. У нас вийшов граф з десятьма вершинами і десятьма ребрами. Потрібно з десяти вибрати п'ять ребер, що не мають спільних вершин.
Гена Діма Вова Боря Алік
Лячпкін- Хлестаков Осип Суниця
Зробити це легко. Досить зауважити, в вершини 3 і 4 веде по одному ребру, з вершин див відповідно. Це означає, що Осипа (вершина 3) повинен грати Діма (хто ж ще), а Суницю-Вова. Вершина 1 Ляпкін- Тяпкин-з'єднана ребрами з Г і Д. Ребро 1 Д відпадає, так як Діма вже зайнятий, залишається ребро 1 Г, Ляпкіна- Тяпкіна повинен грати Гена. Залишається з'єднати вершини А і Б з вершинами 2 і 5, відповідними ролями Хлестакова і Городничого. Це можна зробити двома способами: або вибрати ребра А - 5 і Б-2, або ребра А-2 і Б-5. У першому випадку Алік гратиме Городничого, а Боря-Хлестакова, у другому випадку навпаки. Як показує наш граф, інших рішень завдання не має.
Другий тип завдань. в яких заданий плоский граф потрібно викреслити, не відриваючи олівця від паперу і не обводячи двічі один і той же ділянку графа. Якщо при цьому виходить замкнута лінія, що починається і кінчається в одній і тій же вершині, то такий граф називають ейлерову
Якщо все вершини графа парні то граф можна обійти за один цикл, не проходячи жодного ребра двічі.
Якщо 2 вершини графа непарні, то замкнутого циклу не існує, але можна вийшовши з однієї непарної вершини обійти весь граф і повернутися в другу непарну вершину.
1. Відомий анекдот: Хтось давав 1000000 рублів кожному, хто накреслить наступну фігуру.
Вимога: одним безперервним розчерком т. Е. Не віднімаючи пера або олівця від паперу і не подвоюючи жодної лінії.
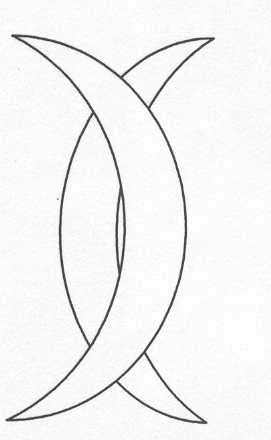
2
. Магомет замість підпису (він був неписьменний) описував одним розчерком що складається з
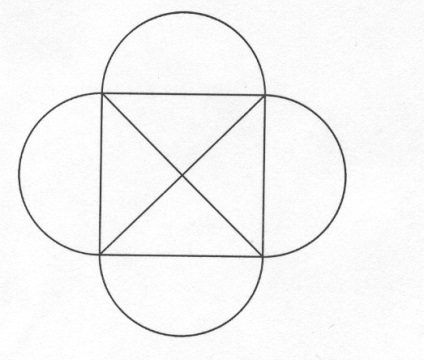
3
. Не можна викреслити одним розчерком фігуру, показану на малюнку 3. Поясни чому
4. Муха забралася в банку з-під цукру. Банку має форму куба. Чи зможе муха послідовно обійти всі 12 ребер куба, не проходячи двічі по одному ребру, Підстрибувати і перелітати з місця на місця на місце не дозволяється.
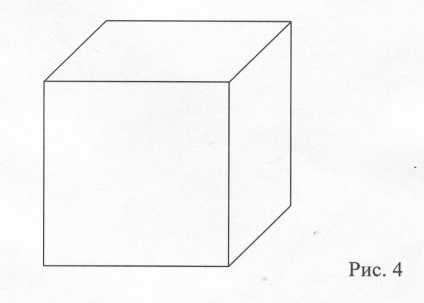
Нивен відзначав: "Математику можна вивчати, спостерігаючи як це робить сусід"
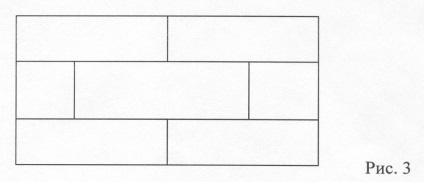
6. Домашнє завдання: Чи можна фігури, зображені на малюнках, намалювати одним розчерком? (Вирішити за допомогою графа)
Сьогодні ми з вами познайомилися ще з одним методом вирішення завдань за допомогою графів.
Повчальна сторона цих завдань полягає в дослідженні, можливо чи ні рішення даного завдання, перш ніж братися за саме рішення.
Ми ще раз переконалися, що теорія графів дозволяє швидко і витончено вирішувати завдання, які досить важко вирішити іншими методами і дозволяє вирішити не тільки одну окремо взяту завдання, але і знаходити шляхи вирішення цілого класу задач.
А на закінчення хочу сказати такі слова: «У завданнях, які ставить перед нами життя, екзаменатором є сама природа.