Виділимо в стаціонарно поточної ідеальної рідини трубку струму малого перетину (рис. 39). Розглянемо обсяг рідини, обмежений стінками трубки струму і перпендикулярними до ліній струму перетинами S1 і S2. За час # 916; t цей обсяг переміститься вздовж трубки струму, причому перетин S1 переміститься в положення S'1. пройшовши шлях # 916; l1. перетин S2 переміститься в положення S'2, пройшовши шлях # 916; l2. В силу нерозривності струменя заштриховані обсяги матимуть однакову величину:
# 916; V1 = # 916; V2 = # 916; V.
Енергія кожної частки рідини складається з її кінетичної енергії і потенційної енергії в поле сил земного тяжіння. Внаслідок стаціонарності ті-чення частка, що знаходиться через час # 916; t в будь-який з точок незаштриховані частини розглянутого обсягу (див. Наприклад, точку О на рис. 39), має таку ж швидкість (а отже, і кінетичну енергію), яку мала частка, яка перебувала в тій же точці в початковий момент часу. Тому приріст енергії # 916; Е досліджуваного обсягу можна обчислити як різницю енергій заштрихованих Об'емчик # 916; V2 і # 916; V1.
Візьмемо перетин трубки струму і відрізки # 916; l настільки малими, щоб усі точки кожного з заштрихованих Об'емчик можна було приписати одне і те ж значення швидкості v, тиску р і висоти h. Тоді приріст енергії запишеться наступним чином:
(# 961; - щільність рідини).
В ідеальній рідині сили тертя відсутні. Тому приріст енергії (98) має дорівнювати роботі, яку здійснюють над виділеним об'ємом силами тиску. Сили тиску на бічну поверхню перпендикулярні в кожній точці до напрямку переміщення частинок, до яких вони включені, внаслідок чого роботи не здійснюють. Відмінна від нуля лише робота сил, прикладених до перетинів S1 і S2. Ця робота дорівнює
Прирівнюючи вирази (98) і (99), скорочуючи на # 916; V і переносячи члени з однаковими індексами в одну частину рівності, отримаємо:
Перетину S1 і S2 були взяті абсолютно довільно. Тому можна стверджувати, що в будь-якому перетині трубки струму вираз має однакове значення. У відповідності зі зробленими нами при його виведенні припущеннями рівняння (100) стає цілком точним лише при прагненні поперечного перерізу S до нуля, т. Е. При стягуванні трубки струму в лінію. Таким чином, величини р, v і h, що фігурують в лівій і правій частинах рівняння (100), слід розглядати як відносяться до двох довільним точкам однієї і тієї ж лінії струму.
Отриманий нами результат можна сформулювати наступним чином: в стаціонарно поточної ідеальної рідини уздовж будь-якої лінії струму виконується умова
Рівняння (101) або рівнозначне йому рівняння (100) називається рівнянням Бернуллі. Незважаючи на те, що це рівняння було отримано нами для ідеальної рідини, воно досить добре виконується для реальних рідин, внутрішнє тертя в яких не дуже велике.
Розглянемо деякі наслідки, що випливають з рівняння Бернуллі. Нехай рідина тече так, що швидкість має в усіх точках однакову величину. Тоді згідно (100) для двох довільних точок будь-якої лінії струму буде виконуватися рівність
звідки випливає, що розподіл тиску в цьому випадку буде таким же, як в спочиває рідини [см. (96)].
Для горизонтальної лінії струму умова (100) приймає вид
,
т. е. тиск виявляється меншим в тих точках, де швидкість більше (якісно це вже було показано в попередньому параграфі).
Застосуємо рівняння Бернуллі до випадку витікання рідини з невеликого отвору в широкому відкритому посуді. Виділимо в рідині трубку струму, що має своїм перетином з одного боку відкриту поверхню рідини в посудині, а з іншого боку - отвір, через який рідина витікає (рис. 40). У кожному з цих перетинів швидкість і висоту над деякими вихідним рівнем можна вважати однаковими, внаслідок чого до них можна застосувати рівняння (100), отримане при цьому припущенні. Далі, тиску в обох перетинах рівні атмосферного і тому однакові. Крім того, швидкість переміщення відкритій поверхні в широкому посудині можна покласти рівною нулю. З урахуванням усього сказаного, рівняння (100) стосовно до даного випадку можна написати у вигляді
,
де v - швидкість витікання з отвору. скорочуючи на # 961; і ввівши h = h1 - h2 - висоту відкритої поверхні рідини над отвором, отримуємо:
,
Ця формула називається формулою Торрічеллі.
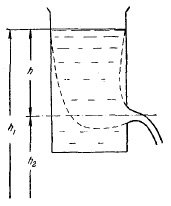
Витікання рідини з отвору
Отже, швидкість витікання рідини з отвору, розташованого на глибині h під відкритою поверхнею, збігається зі швидкістю, яку набуває будь-яке тіло, падаючи з висоти h.
Слід пам'ятати, що цей результат отримано в припущенні, що рідина ідеальна. Для реальних рідин швидкість витікання буде менше, причому тим сильніше відрізняється від значення (102), чим більше в'язкість рідини.