Рівняння Ейлера - це рівняння гідродинаміки, яке описує рух потоку ідеальної рідини і враховує сили, що впливають на рідину.
У моделі Ейлера розглядається ідеальна рідина, в якій відсутні теплопровідність (рідина має постійну температуру, не нагрівається і не охолоджується) і в'язкість (в рідини не виникають сили тертя). Тому сили, що впливають на таку рідину, зводяться до сил тиску її власних мас, гравітаційним і інерційним силам.
Рівняння Ейлера в векторній формі
У векторній формі рівняння Ейлера має вигляд:
Складові в правій частині враховують вплив зовнішніх сил і тиску власної маси рідини: - напруженість зовнішнього силового поля, - тиск в рідині, - щільність рідини. Вектор - швидкість руху рідини. - субстанциональная похідна, яка представляє собою прискорення рухається точки в матеріальному середовищі. Субстанциональную похідну можна розкласти на приватні похідні. і тоді рівняння Ейлера набуде вигляду:
Останнє рівняння ще називають рівнянням руху нев'язкої рідини в формі Громеко. Воно зручно ще й тим, що виділяє вихревую складову руху у вигляді доданка, а приватна похідна по часу відображає місцеве прискорення, характерне для несталих течій.
Рішення рівняння Ейлера
При розрахунках зручніше використовувати рівняння Ейлера в скалярною формі:
де вектори швидкості і зовнішніх сил, а також поле тиску розкладені у вигляді проекцій на координатні осі.
При вирішенні нескладних прикладних задач гідро- і газодинаміки іноді буває досить розглянути сталий в часі одновимірний потік. У цьому випадку рівняння Ейлера прийме простою вигляд:
Проинтегрировав цей вислів, можна отримати рівняння Бернуллі:
Рівняння Ейлера, що лежить в основі гідродинаміки, використовується в самих різних областях: при проектуванні літаків і суден, при розрахунку турбін, насосів і трубопроводів, при дослідженні морських течій і руху ґрунтових вод.
Приклади розв'язання задач
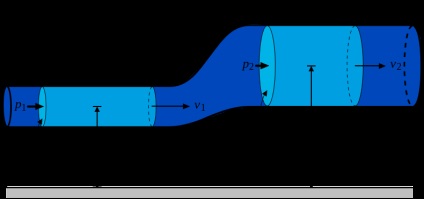
По горизонтальній трубі протікає рідина щільністю 950 кг / м 3. Тиск на вході в трубу 0,3 МПа, на виході з труби 1 МПа. Швидкість на вході в трубу 50 м / с. Визначити швидкість на виході з труби.
Запишемо рівняння Ейлера для стаціонарного одновимірного потоку:
Помножимо обидві частини на dx і проинтегрируем:
Запишемо цей вираз для вхідного і вихідного перерізів: