Знайдемо кінематичний закон прямолінійного рівноприскореного руху. Для цього використовуємо формули (1.6), (1.11) і (1.13). З них випливає, що s = vср · t = (v0 + v) · t / 2 = (2v0 + at) · t / 2,
отже,
Якщо початкова швидкість тіла дорівнює нулю (v0 = 0), то
За формулами (1.14) і (1.15) визначають шлях, пройдений тілом в равноускоренном прямолінійній русі (модуль переміщення тіла, що не зраджує напрямки свого руху). Для випадку, коли тіло рухається по осі Ох .з точки з координатою х0. з формули (1.14) отримуємо рівняння, що виражає залежність координати цього тіла від часу. оскільки
Формула (1.16) є рівняння прямолінійного рівноприскореного руху (кінематичний закон цього руху). Слід пам'ятати, що у формулі (1.16) v0x і аx можуть бути як позитивними, так і негативними, так як це проекції векторів v0 і а на вісь Ох.
При поступальному русі тіла всі точки тіла рухаються однаково, і, замість того щоб розглядати рух кожної точки тіла, можна розглядати рух тільки однієї його точки.
Основні характеристики руху матеріальної точки: траєкторія руху, переміщення точки, пройдений нею шлях, координати, швидкість і прискорення.
Лінію, по якій рухається матеріальна точка в просторі, називають траєкторією.
Система відліку - це сукупність тіла відліку, системи координат і системи відліку часу, пов'язаних з цим тілом, по відношенню до якого вивчається рух (або рівновага) будь-яких інших матеріальних точок або тел.Математіческі рух тіла (або матеріальної точки) по відношенню до вибраній системі відліку описується рівняннями, які встановлюють, як змінюються з плином часу t координати, що визначають положення тіла (точки) в цій системі відліку. Ці рівняння називаються рівняннями руху. Наприклад, в декартових координатах х, y, z рух точки визначається рівняннями x = f1 (t), y = f2 (t), z = f3 (t) .В сучасній фізиці будь-який рух є відносним, і рух тіла слід розглядати лише по відношенню до будь-якого іншого тіла (тіла відліку) або системі тіл. Не можна вказати, наприклад, як рухається Місяць взагалі, можна лише визначити її рух, наприклад, по відношенню до Землі, Сонцю, зіркам і т. П.
5.Двіженіе точки по колу. Швидкість і прискорення при криволінійному русі. Нор-мальное і дотичне прискорення.
Рух по колу є досить поширеним в навколишньому світі: при обертанні будь-якого твердого тіла навколо фіксованої осі всі крапки цього тіла рухаються по колах. Так як всі кола подібні, то досить описати рух однієї з них, щоб описати обертання всього твердого тіла. Крім того, рівномірний рух по колу є найпростішим криволінійним рухом.
Нехай матеріальна точка рухається з постійною за модулем швидкістю v по колу радіуса R.
Рух тіла по колу є окремим випадком криволінійного руху. Поряд з вектором переміщення зручно розглядати кутове переміщення # 916; # 966; (Або кут повороту), яка вимірюється в радіанах (рис. 1.6.1). Довжина дуги пов'язана з кутом повороту співвідношенням
При малих кутах повороту # 916; l ≈ # 916; s.
У цій формулі # 916; # 965; # 964; = # 965; 2 - # 965; 1 - зміна модуля швидкості за проміжок часу # 916; t.
Напрямок вектора повного прискорення визначається в кожній точці кругової траєкторії величинами нормального і дотичного прискорень.
Швидкість і прискорення при криволінійному русі.
Криволінійний рух складніший вид руху, ніж прямолінійний, оскільки навіть якщо рух відбувається на площині, то змінюються дві координати, що характеризують положення тіла. Швидкість і прискорення тіла також постійно змінюються по напрямку, а в загальному випадку і по модулю. Миттєва швидкість тіла при криволінійному русі спрямована в будь-якій точці траєкторії по дотичній до траєкторії в цій точке.Етот висновок про направлення миттєвої швидкості можна підтвердити, спостерігаючи, як рухаються бризки з # 8209; під коліс буксує автомобіля або іскри при заточуванні деталей на обертовому точильному камені При криволінійному русі напрям швидкості тіла змінюється, тому такий рух є нерівномірним, навіть якщо модуль швидкості залишається постійним.
Прискорення при криволінійному русі.
Розглядаючи криволінійний рух тіла, ми бачимо, що його швидкість в різні моменти різна. Навіть в тому випадку, коли величина швидкості не змінюється, все ж має місце зміна напрямку швидкості. У загальному випадку змінюються і величина, і напрямок скорості.Такім чином, в криволінійному русі завжди є зміна швидкості, т. Е. Це рух відбувається з прискоренням. Для визначення цього прискорення (за величиною і напрямком) потрібно знайти зміна швидкості як вектора, т. Е. Потрібно знайти зміна величини і зміну напрямку скорості.Пусть, наприклад, точка, рухаючись криволинейно (рис. 49), мала в певний момент швидкість v1 а через малий проміжок часу - швидкість v2. Зміна швидкості є різниця між векторами v1 і v2. Так як ці вектори мають різне спрямування, то потрібно взяти їх векторну різницю. Зміна швидкості виразиться вектором w, зображуваних стороною паралелограма з діагоналлю v2 і іншою стороною v1. Прискоренням ми називаємо відношення зміни швидкості до проміжку часу, за який ця зміна відбулася. Значить, прискорення а так само
і по напрямку збігається з вектором w.
Вибираючи t досить малим, прийдемо до поняття векторного миттєвого прискорення (пор. § 16); при довільному t вектор а представлятиме середнє прискорення за проміжок часу t.Направленіе прискорення криволінійного руху не збігається з напрямком швидкості, в той час як для прямолінійного руху ці напрямки збігаються. Щоб знайти напрям вектора прискорення при криволінійному русі, досить зіставити напрямки швидкостей в двох близьких точках траєкторії. Так як швидкості спрямовані по дотичним до траєкторії, то з вигляду самої траєкторії можна зробити висновок, в який бік від траєкторії направлено прискорення. Дійсно, так як різниця швидкостей в двох близьких точках траєкторії завжди спрямована в ту сторону, куди викривляється траєкторія, то, значить, і прискорення при криволінійному русі завжди направлено в сторону угнутості траєкторії. Наприклад, коли кулька котиться по вигнутому жолобу (рис. 50), його прискорення на ділянках АВ і ВС завжди направлено так, як показують стрілки, причому це не залежить від того, котиться кулька від A до С або в зворотному напрямку.
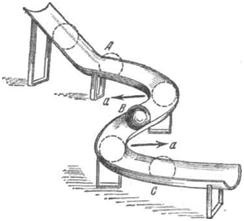
Мал. 50. Прискорення при криволінійному русі завжди спрямовані в бік угнутості страекторіі.
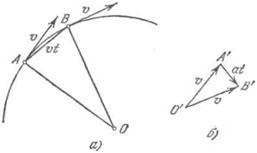
Мал. 51. До висновку формули для центростремительного прискорення.
Розглянемо рівномірний рух точки по криволінійній траєкторії. Ми вже знаємо, що це - прискорений рух. Знайдемо прискорення. Для цього достатньо розглянути прискорення для окремого випадку рівномірного руху по колу. Візьмемо два близьких положення А і В, що рухається точки, відповідні малому проміжку часу t (рис. 51, а). Швидкості рухається точки в А і В рівні за величиною, але різні за напрямком.
Знайдемо різницю цих швидкостей, користуючись правилом трикутника (рис. 51, б). Трикутники ОАВ і О'А'В 'подібні, як трикутник з рівними кутами при вершині. Довжину боку А'В ', яка зображує приріст швидкості за проміжок часу t, можна покласти рівною at, де а - величина шуканого прискорення. Подібна їй сторона АВ є хорда дуги АВ; внаслідок малості дуги довжина її хорди може бути наближено прийнята рівною довжині дуги, т. е. vt. Далі, 0'A '= 0'B' = v; ОА = OB = R, де R - радіус траєкторії. З подоби трикутників випливає, що відносини подібних сторін в них рівні:
звідки знаходимо шукане прискорення за величиною:
Напрямок прискорення перпендикулярно до хорди АВ. Для досить малих проміжків часу можна вважати, що дотична до дуги практично збігається з її хордою. Значить, знайдене прискорення можна вважати спрямованим перпендикулярно ( «нормально») до дотичній до траєкторії, т. Е. По радіусу, до центру кола. Тому таке прискорення називають нормальним або доцентрові прискоренням.
Якщо траєкторія - НЕ окружність, а довільна крива лінія, то у формулі (27.1) слід взяти радіус кола, найближче підходить до кривої в даній точці. Напрямок нормального прискорення і в цьому випадку буде нормально до дотичній до траєкторії в даній точці. Якщо при криволінійному русі прискорення постійно по величині і напрямку, його можна знайти як відношення приросту вектора швидкості до проміжку часу, за який це збільшення відбулося, яким би не був цей проміжок часу. Значить, в цьому випадку вектор прискорення можна знайти по векторної формулою
аналогічною формулою (18.1) для прямолінійного руху з постійним прискоренням. Тут v0 - вектор швидкості тіла в початковий момент проміжку часу t, a v - вектор швидкості в кінцевий момент цього промежутка.Нормальное прискорення - це складова вектора прискорення, спрямована уздовж нормалі до траєкторії руху в даній точці на траєкторії руху тіла. Тобто вектор нормального прискорення перпендикулярний лінійної швидкості руху (див. Рис. 1.10). Нормальне прискорення характеризує зміну швидкості у напрямку і позначається буквою n. Вектор нормального прискорення спрямований по радіусу кривизни траекторіі.Тангенціальное (дотичне) прискорення - це складова вектора прискорення, спрямована уздовж дотичній до траєкторії в даній точці траєкторії руху. Тангенціальне прискорення характеризує зміну швидкості по модулю при криволінійному русі.
Мал. 1.10. Тангенціальне прискорення.
Напрямок вектора тангенціального прискорення # 964; (Див. Рис. 1.10) збігається з напрямком лінійної швидкості або протилежно йому. Тобто вектор тангенціального прискорення лежить на одній осі з дотичного кола, яка є траєкторією руху тіла.