Обсяг одного квантового стану в фазовому просторі. Функція щільності енергетичних станів.
Щоб обчислювати щільність станів енергії для частинки, ми спочатку обчислимо щільність станів в зворотному просторі (імпульсна або k-простір). Відстань між станами задано граничними умовами. Для вільних електронів і фотонів в межах ящика розміру L, і для електронів в кристалічній решітці з розміром решітки L використовуємо періодичні граничні умови Борна - фон Кармана. Використовуючи хвильову функцію вільної частинки отримуємо
2 \ pi n = kL \\
\ frac = \ Delta k \\
де n - будь-яке ціле число, а \ Delta k \, - відстань між станами з різними k.
Загальна кількість k-станів, доступних для частки - обсяг k-простору доступного для неї, розділеного на обсяг k-простору, займаного одним станом. Доступний обсяг - просто інтеграл від k = 0 до k = k. Обсяг k-простору для одного стану в n-вимірному випадку запишеться у вигляді
g_s - виродження рівня (зазвичай це спіновий виродження, рівне 2). Цей вислів потрібно продифференцировать, щоб знайти щільність станів в k-просторі: g (k) \, dk = \ frac \, dk. Щоб знайти щільність станів по енергії, потрібно знати закон дисперсії для частинки, тобто висловити k і dk в вираженні g (k) dk в термінах E і dE. Наприклад для вільного електрона: E = \ frac = \ frac, dE = \ frac \, dk.З більш загальним визначенням пов'язано співвідношення
де індекс s відповідає деякому станом дискретного або безперервного спектра, а \ delta - дельта-функція Дірака. При переході від підсумовування до інтегрування слід керуватися правилом
де \ hbar - постійна Планка.
Ідеальний Фермі-газ. Зв'язок енергії Фермі та концентрації електронів.
Ідеальний Фермі-газ. Середня енергія електрона.
Види зв'язків атомів і молекул в кристалах. Аморфне і кристалічна стану. Кристалічна решітка. Період решітки. Стану електронів в кристалі. Поняття квазіімпульса.
Модель Кроніга-Пені. Хвильова функція електрона.
Модель Кроніга-Пені. Енергетичні зони. Зони Бріллюена. Зв'язок енергетичних зон і рівнів енергії електрона в потенційній ямі з нескінченно високими стінками.
Класифікація кристалів за структурою енергетичних зон. Зона провідності і валентна зона. Ефективна маса електрона і дірки.
Визначення власного напівпровідника. Виникнення електропровідності власного напівпровідника з точки зору модельних уявлень і зонної теорії. Розрахунок концентрації електронів в зоні провідності довільного напівпровідника.
23. Визначення власного напівпровідника. Виникнення електропровідності власного напівпровідника. Умова електронейтральності. Розрахунок рівня Фермі і питомої електропровідності власного напівпровідника. Графіки n = f (T), # 61555; # 61472; # 61501; # 61472; f (Т), Ln # 61555; # 61472; # 61501; # 61472; f (1 / T). Експериментальне визначення ширини ЗЗ.
Обидва процеси - генерація пар носіїв заряду і їх рекомбінація - в будь-якому обсязі напівпровідника відбуваються одночасно. Відповідна концентрація носіїв заряду встановлюється з умови динамічної рівноваги, при якому число знову виникаючих носіїв заряду дорівнює числу рекомбінуючих. Проміжок часу між моментом генерації носія заряду і його рекомбінацією називають часом життя вільного електрона або дірки, а пройдена носієм заряду за час життя відстань - довжиною вільного пробігу. З огляду на, що час життя окремих носіїв заряду по-різному, під цими термінами розуміють середній час життя і середню довжину вільного пробігу.
ровень Фермі - основний параметр статистичного розподілу електронів і дірок. У розрахунках для визначення положення рівня Фермі, як правило, використовують умова електронейтральності.
Для власного полупроводнікаn = p.
При розрахунку власної концентрації необхідно враховувати залежність ширини забороненої зони від температури (1.17). Власна концентрація є важливим характеристичним параметром матеріалу, оскільки для заданої температури ni 2-величина постійна не тільки для власних, а й для легованих матеріалів (вона не залежить від положення рівня Фермі). Значення власної концентрації для основних напівпровідникових матеріалів представлені в таблиці.
24. Визначення донорного напівпровідника і донорної домішки. Електропровідність донорного напівпровідника при високих і низьких температурах. Температура примесного виснаження. Умова електронейтральності. Графіки n = f (T), # 61555; # 61472; # 61501; # 61472; f (Т), Ln # 61555; # 61472; # 61501; # 61472; f (1 / T). в широкому інтервалі температур.
Донорний провідник і донорная домішка. Електропровідність донорного провідника при високій і низькій температурі. Умови електронейтральності.
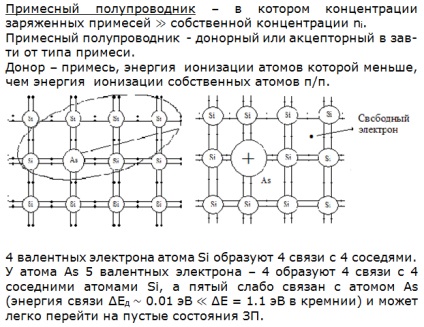


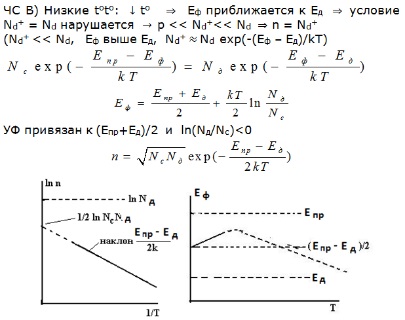
25. Розрахунок рівня Фермі донорного напівпровідника. Розрахунок питомої електропровідності донорного напівпровідника. Графіки n = f (T), # 61555; # 61472; # 61501; # 61472; f (T), Ln # 61555; # 61472; # 61501; # 61472; f (1 / T) в широкому інтервалі температур.

Рівноважна концентрація. Зв'язок концентрацій електронів і дірок у власному і домішковому напівпровідниках. Ефект придушення.
Розглянемо загальний випадок, коли концентрація дрібних донорів відрізняється від концентрації дрібних акцепторів. Для визначеності покладемо, що. В цьому випадку дрібні донори і дрібні акцептори в кількості будуть взаємно компенсовані, тобто всі акцептори будуть заповнені електронами прийшли з донорних центрів, отже,. Число некомпенсованих донорів здатних брати участь у тепловій генерації електронів в с - зону дорівнюватиме: - ефективна концентрація донорів. Значить, при співвідношенні напівпровідник веде себе як напівпровідник - типу. В такому напівпровіднику немає домішкових дірок, а є дірки утворюються в результаті власних переходів при високих температурах. Рівняння електронейтральності для такого напівпровідника з урахуванням попереднього параграфа матиме вигляд:
Розглянемо кілька бокові випадків.
1. Дуже низькі температури.
В цьому випадку . . Тоді рівняння електронейтральності набуде вигляду:
Підставами (3) в вираз для. отримаємо:
- концентрація донорів зайнятих електронами.
- ефективна концентрація іонізованих донорів.
Таке рівняння вирішено в §4.
Видно, що енергія активації.
3. Високі температури.
У цьому випадку не можна нехтувати величиною. . Тоді рівняння електронейтральності набуде вигляду:
Рішення цього рівняння в §5. При високих температурах:
За величиною . в цій області можна визначити ефективну концентрацію.
4. Дуже високі температури.
27. Швидкість генерації. Теплова генерація. Швидкість рекомбінації. Коефіцієнт рекомбінації. Рівноважний і стаціонарне стану. Надмірна концентрація. Закон убутку надлишкової концентрації згодом. Час життя неосновних носіїв. Графіки D р (t). р (t) (або Dn (t). n (t).
Під дією прикладеного до кристалу напруги в ньому виникає електричне поле. Рух носіїв заряду впорядковується: електрони переміщаються у напрямку до позитивного електрода, дірки - до негативного. При цьому не припиняється і тепловий рух носіїв заряду, внаслідок якого відбуваються зіткнення їх з атомами напівпровідника і домішки.
Направлений рух носіїв заряду під дією сил електричного поля називають дрейфом. а викликаний цим рухом ток - дрейфовим струмом. При цьому характер струму може бути електронним, якщо він викликаний рухом електронів, або дірковим, якщо він створюється спрямованим переміщенням дірок.
Середня швидкість носіїв заряду в електричному полі прямо пропорційна напруженості електричного поля:
Коефіцієнт пропорційності m називають рухливістю електронів (mn), або дірок (mp). Вільні електрони рухаються в просторі між вузлами кристалічної решітки, а дірки - по нековалентним зв'язків, тому середня швидкість, а отже, і рухливість електронів більше, ніж дірок. У кремнію рухливість менше, ніж у германію.
У власних напівпровідниках концентрації електронів і дірок однакові, але внаслідок їх різної рухливості електронна складова струму більше доречний. У домішкових напівпровідниках концентрації електронів і дірок істотно відрізняються, характер струму визначається основними носіями заряду: в напівпровідниках р-типу - дірками, а в напівпровідниках n-типу - електронами.
При нерівномірної концентрації носіїв заряду ймовірність їх зіткнення один з одним більше в тих шарах напівпровідника, де їх концентрація вище. Здійснюючи хаотичний тепловий рух, носії заряду відхиляються в сторону, де менше число зіткнень, тобто рухаються в напрямку зменшення їх концентрації.
Направлений рух носіїв заряду з шару з більш високою їх концентрацією в шар, де концентрація нижче, називають дифузією. а струм, викликаний цим явищем, - дифузійним струмом. Цей струм, як і дрейфовий, може бути електронним чи дірковим.
Ступінь нерівномірності розподілу носіїв заряду характеризується градієнтом концентрації; його визначають як відношення зміни концентрації до зміни відстані, на якому воно відбувається. Чим більше градієнт концентрації, тобто чим різкіше вона змінюється, тим більше дифузний струм.
Електрони, переміщаючись з шару з високою концентрацією в шар з більш низькою концентрацією, у міру просування рекомбинируют з дірками, і навпаки, диффундирующие в шар зі зниженою концентрацією дірки рекомбінують з електронами. При цьому надмірна концентрація носіїв заряду зменшується.