Премія, яка розраховується на основі принципу еквівалентності і забезпечує його дотримання, називається "ризикова премія". Вона відповідає вартості того окремого ризику, який страховик приймає на себе за договором страхування.
Для виведення формул розрахунку ризикової премії на основі принципу еквівалентності спочатку проводиться оцінка очікуваної вартості зобов'язань сторін. Прирівнюючи їх, отримують рівняння, де величина премії в зобов'язаннях страхувальника є невідомим. В результаті його рішення в загальному вигляді отримують необхідні розрахункові залежності. Проілюструємо це на невеликому прикладі.
Приклад. Еквівалентна вартість ризику
У попередньому прикладі ризик автовласника до його участі в страховому фонді було таке: чи з певною ймовірністю q він міг втратити автомобіль вартістю s; а з ймовірністю (1 - q) він нічого не втрачав, тобто його збитки були рівні 0.
Цей ризик автовласник передав страховому фонду. Очікувана вартість такого ризику за визначенням математичного очікування дорівнює сумі творів можливих значень випадкової величини на ймовірність їх настання, тобто
За передачу ризику власник автомобіля сплатив до страхового фонду певну суму (страхову премію) П. Ця премія підлягала сплаті безумовно при вступі до фонду, тому витрати автовласника в будь-якому випадку складали П. Відбувся обмін випадкового ризику настання катастрофічного збитку (розкрадання автомобіля) на фіксований ( невипадковий) збиток, рівний страхової премії.
Даний обмін повинен будуватися на еквівалентній основі. Принцип еквівалентності, що лежить в основі передачі ризику в страхуванні, має на увазі рівність очікуваних вартостей зобов'язань сторін. Це означає, що очікувана вартість премій за договором повинна бути дорівнює очікуваної вартості виплат. У нашому випадку премія сплачується безумовно, її очікувана вартість дорівнює фактичній, тому можна записати
Якщо підставити числові значення з попереднього прикладу, то отримуємо вже знайомий результат:
Розрахована таким чином величина премії є справедливою платою за страхування, еквівалентній того ризику, який передає даний учасник в страховий фонд.
У розглянутому прикладі термін страхування становив всього один рік, і принцип еквівалентності застосовувався в спрощеній формулюванні, що не враховувала зміну вартості грошей у часі та додатковий дохід від інвестування. Крім того, страхова премія в обов'язковому порядку повністю сплачувалася в момент початку страхування. Тому її очікувана вартість збігалася з фактичною. В результаті ризикова премія виявилася рівною очікуваній вартості виплат за договором:
Подібна ситуація характерна для більшості видів майнового та особистого страхування, крім страхування життя.
Якщо кожна ризикова премія еквівалентна очікуваному збитку за договором, то їх сума буде дорівнює очікуваної сукупної величиною виплат по всьому портфелю. Тобто чисті справедливі премії є достатніми, якщо фактична сума виплат не перевищить очікувану. Але на практиці можуть мати місце відхилення від очікуваних значень як в меншу, так і в більшу сторону. Подібні коливання є наслідком дії особливих ризиків, які виникають в результаті об'єднання договорів в один портфель.
Перш за все, для будь-якого страхового портфеля завжди існує ризик випадковості. Навіть якщо відомі об'єктивно існуючі теоретичні ймовірності настання страхових випадків і розподіл виплат, передбачити конкретні значення, які візьмуть випадкові величини, неможливо (тому вони і називаються випадковими). Навіть для величезних сукупностей закон великих чисел не гарантує рівності фактичних середніх величин очікуваним. Він лише дозволяє оцінити інтервал, в який із заданою вірогідністю потрапить це значення. Ширина такого інтервалу залежить від кількості ризиків в портфелі. Чим їх більше, тим менш імовірні великі відхилення від очікуваних значень. Але така ймовірність, нехай і дуже мала, завжди існує.
При розрахунку ризикових премій орієнтуються на очікувані значення. Але ніхто не знає справжніх (теоретичних) очікуваних значень кількості страхових випадків і збитків ні для окремого договору, ні для портфеля в цілому. На практиці їх доводиться оцінювати на основі наявної статистики. Отримувані оцінки завжди в тій чи іншій мірі відрізняються від істинного значення. Це привносить в діяльність страхової компанії додаткову невизначеність, яку називають ризиком оцінки.
Статистичні дані, на основі яких оцінюються випадкові величини, зібрані в минулих періодах. Однак в майбутньому рівень "небезпеки" може змінитися. Це відноситься до всіх областей людського життя. Кліматичні зміни впливають на ймовірність природних катастроф. Завдяки науковому прогресу з'являються нові види техніки, властивості яких ще погано вивчені. Розвиток медицини знижує ризик смертності та збільшує тривалість життя. Тому тарифи, розраховані методично вірно по абсолютно надійним оцінками, можуть виявитися недостатніми. Потрібно прогнозування зміни рівня "небезпек" в часі. В результаті виникає так званий ризик прогнозу.
Всі три складові невизначеності, властиві страхуванню, об'єднуються загальним поняттям "технічний страховий ризик". Через його наявності в діяльності кожного страховика завжди є ймовірність несприятливого відхилення фактичної суми збитків по портфелю від її очікуваної величини. Для компенсації можливих відхилень страхова компанія може використовувати власні або позикові кошти або заздалегідь сформовані спеціальні резерви. Одним з основних джерел коштів покриття даного ризику є ризикова (або гарантійна) надбавка.
Для випадкової величини ймовірність прийняти значення більше або менше математичного очікування рівні 50%. Тому ризикова премія, яка орієнтується на очікувані значення, буде достатня лише в половині випадків. Доповнення її ризикової надбавкою збільшує ймовірність беззбиткової роботи компанії до деякого заданого страховиком рівня, який називається "гарантія безпеки".
Її практична величина знаходиться в межах від 95 до 99,99%, але ніколи не може досягти 100%. Це можна пояснити наступним чином. Якщо страховик хоче абсолютно достовірно забезпечити перевищення премій над виплатами, він повинен сформувати страховий фонд у розмірі сукупної страхової суми. В цьому випадку премія за кожним договором дорівнюватиме страхової суми. Зрозуміло, такі умови є неприйнятними для страхувальників. Тому компанії змушені приймати гарантію безпеки менше 100%, хоча і досить близьку до неї. Таким чином, навіть введення в премію ризикової надбавки може гарантувати беззбитковість роботи тільки з деякою, нехай і дуже великий, ймовірністю.
Приклад. ризикова надбавка
У попередніх прикладах ми розглядали портфель зі страхування автомобілів на випадок розкрадання, що підкоряється дії закону великих чисел. Для оцінки кожного окремого ризику використовуються очікувані значення збитків. Тим самим забезпечується еквівалентність зобов'язань сторін. Але наскільки можна бути впевненим, що даних премій вистачить на все виплати?
Портфель складається з п = 1000 договорів. Розмір збитку при страховому випадку фіксований і відповідає вартості автомобіля s = 500 000 руб. Тому загальна сума виплат по портфелю визначається однією випадковою величиною - кількістю розкрадань. За кожним договором страховий випадок може наступити з імовірністю q = 0,03. Якщо всі договори незалежні, то число викрадень в такому портфелі є дискретною випадковою величиною, розподіленою за біноміальним законом.
Ризикова премія за договором була визначена в розмірі
0,03 x 500 000 = 15 000 руб.
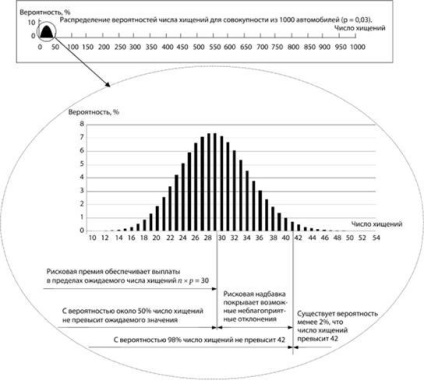
Мал. 5.1. Ілюстрація до розрахунку ризикової надбавки
Їх суми вистачить на виплати, якщо число викрадень не перевищить очікуваного значення, що дорівнює
Імовірність цієї події (m = 30), визначена за біноміальним законом, дорівнює 55%. В інших 45% випадків число викрадень виявиться вище очікуваного, і ризикових премій буде недостатньо. Зрозуміло, для практичної роботи такий рівень безпеки неприйнятний. Потрібно ризикова надбавка, яка забезпечить компенсацію можливих несприятливих відхилень фактичних виплат від очікуваних і тим самим підвищить ймовірність беззбиткової роботи до заданого рівня гарантії безпеки 98-99,99%.
Для розглянутого портфеля ризиків кількість викрадень, яке з ймовірністю 98% не буде перевищено, становить 42. При гарантії безпеки, що дорівнює 99,99%, це значення збільшується до 52 (рис. 5.1)!
Якщо встановлений рівень безпеки 98%, розмір фонду повинен бути достатнім для оплати 42 викрадень. Ризикові премії гарантують виплату лише за очікуваними 30 страховими випадками. Ризикова надбавка повинна дати можливість страхової компанії, якщо буде потрібно, здійснити ще 12 виплат.
Сума ризикової надбавки, яка припадає на один договір, складе
12 x 500 000/1000 = 6000 руб.
Тоді страхова премія, яка забезпечить можливість неразоренние 98%, повинна бути дорівнює
15 000 + 6000 = 21 000 руб. замість 15 000 руб. "Чистої" премії.
По відношенню до ризикової премії надбавка становить
6000/15000 = 0,4 = 40%.
Це значна величина. Якщо ж страховику вдалося в одному портфелі об'єднати НЕ 1000 ризиків, а 5000, то при тому ж рівні безпеки 98% надбавка складе вже 2500 руб. на договір, тобто всього близько 17% від ризикової премії. Для портфеля з 10 000 договорів її величина зменшиться до 12%.
Даний ефект проявляється в результаті дії закону великих чисел. Чим більше безліч випадкових величин, тим менш імовірні відхилення середніх значень від очікуваних. Для страхової компанії збільшення портфеля означає можливість зробити менше надбавку до премії і тим самим знизити ціну страхування. Це дає серйозна конкурентна перевага великим страховим компаніям.
Завдання розрахунку ризикової надбавки досить складна. Для її вирішення необхідно, по-перше, визначити необхідну загальну суму ризикових надбавок і, по-друге, встановити "справедливий" принцип поділу цієї загальної суми між усіма договорами.
У розглянутому прикладі загальна сума ризикових надбавок визначалася на основі припущення про біноміальний розподіл сукупного збитку по портфелю. Потім вона ділилася порівну між усіма учасниками, оскільки за умовами всі застраховані ризики були однакові. На практиці в портфелі об'єднуються різні за ступенем "небезпеки" договори, і сукупний збиток може мати більш складний розподіл. Тому існують різні підходи до поділу надбавки: принцип математичного очікування (тобто пропорційно ризикової премії), принцип середнє відхилення, принцип дисперсії і т.д. Можливі також їх комбінації.
Величина ризикової надбавки залежить від заданого рівня гарантії безпеки і розкиду сукупного збитку щодо очікуваного значення. Останній, в свою чергу, визначається кількістю договорів в портфелі і дисперсією (среднеквадратическим відхиленням) ризиків, що становлять цей портфель.
Якщо Ви помітили помилку в тексті виділіть слово і натисніть Shift + Enter