Слідкуйте за виходом нових статей цієї серії.
Цей контент є частиною серії: Робота зі структурами даних в мовах Сі та Python
Слідкуйте за виходом нових статей цієї серії.
Бінарні (двійкові) дерева є одним з найбільш затребуваних варіантів даної структури даних, так як широко використовуються в пошукових алгоритмах і для вирішення інших обчислювальних задач. У даній статті будуть розглянуті основні характеристики бінарних дерев і різні операції, що виконуються над ними.
Як завжди, крім теоретичних аспектів: класифікації бінарних дерев і стандартних прийомів для маніпулювання ними, в статті будуть приклади практичної реалізації алгоритмів для роботи з бінарними деревами на мовах Сі та Python.
Класифікація бінарних дерев
Перед тим, як перейти до обговорення різних типів бінарних дерев, варто зупинитися на загальній класифікації пошукових алгоритмів.
У випадку з лінійним пошуком шуканий елемент порівнюється з кожним елементом списку в ході послідовної ітерації. Швидкість такого пошуку залежить від розміру списку: чим більше список, тим нижче швидкість, тобто швидкість обернено пропорційна розміру списку. Збільшити швидкість такого пошуку можна, якщо попередньо відсортувати список. У цьому випадку вже не буде потрібно продовжувати пошук, коли шуканий елемент ще не буде знайдений, а елементи в списку вже стануть більше шуканого.
Для відсортованого списку існує і більш ефективний алгоритм. На початку пошуку необхідно порівняти дані число з елементом, який знаходиться посередині вже відсортованого списку. Якщо серединний елемент виявляється більше шуканого числа, значить шуканий елемент знаходиться в лівій половині. В іншому випадку - справа. Потім виконується порівняння з числом, яке знаходиться посередині потрібної половини. І так далі до тих пір, поки не буде знайдено шукане число. Даний тип пошуку називається двійковим. і він, очевидно, швидше лінійного. Необхідна кількість поділів списку, що складається з n елементів навпіл, називається логарифмом від n по підставі 2. Двійковий пошук є алгоритмом порядку O (log) за основою 2.
Однак традиційні зв'язкові списки не дуже підходять для двійкового пошуку, і тут на допомогу приходить двоичное дерево, приклад якого зображений на малюнку 1.
Малюнок 1. Приклад двійкового дерева
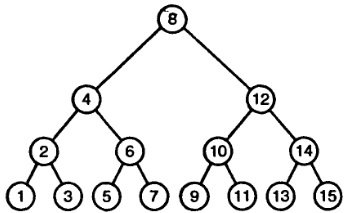

У загальному випадку кожен вузол в дереві може мати необмежену кількість дочірніх вузлів. Відмінність бінарного дерева від інших типів дерев в тому, що кожен вузол в ньому може мати не більше двох дочірніх вузлів. Звичайне двоичное дерево - це структура, що складається з вузлів, кожен з яких містить деяке значення, а також покажчики на ліве і праве піддерева. Один або обидва покажчика на ці піддерева можуть мати значення NULL. Двійкові дерева, як і зв'язкові списки, є рекурсивними структурами.
На малюнку 2 показані бінарні дерева, які мають однаковий набір вузлів, але різний порядок їх слідування. В останньому випадку дерево вироджується в зв'язний список.
Малюнок 2. Різні реалізації одного і того ж бінарного дерева
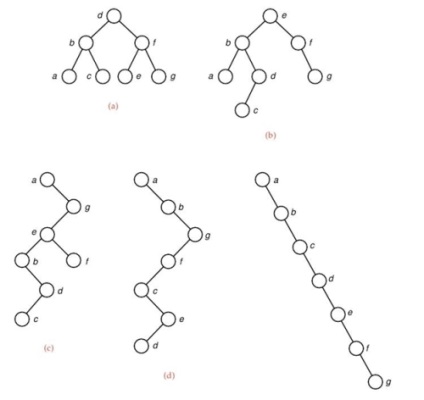

Існують такі різновиди бінарних дерев:
- повне бінарне дерево - кожен вузол, за винятком листя, має по 2 дочірніх вузла;
- ідеальне бінарне дерево - це повне бінарне дерево, в якому все листя знаходяться на одній висоті;
- збалансоване бінарне дерево - це бінарне дерево, в якому висота 2-х піддерев для кожного вузла відрізняється не більше ніж на 1. Глибина такого дерева обчислюється як двійковий логарифм log (n), де n - загальне число вузлів;
- вироджене дерево - дерево, в якому кожен вузол має всього один дочірній вузол, фактично це зв'язний список;
- бінарне пошукове дерево (BST) - бінарне дерево, в якому для кожного вузла виконується умова: всі вузли в лівому поддереве менше, і всі вузли в правому поддереве більше даного вузла.
обчислення шляхів
Шлях (англ. Path) - це відстань від кореня дерева до будь-якого вузла. У розширеному бінарному дереві кожен шлях закінчується листом. Якщо число листя позначити як S. а число інших вузлів позначити як N. то справедлива формула:
тобто для розширеного дерева число листя на одиницю більше числа НЕлістьев (вузлів, що мають дочірні вузли).
Якщо шлях від кореневого вузла до листа позначити як зовнішній шлях, а шлях від кореневого вузла до НЕліста позначити як внутрішній шлях, тоді сума всіх зовнішніх шляхів для дерева, зображеного на малюнку 3 дорівнює:
а сума внутрішніх шляхів буде дорівнює:
і тоді буде справедлива формула:
де n - число внутрішніх вузлів (НЕлістьев).
Малюнок 3. Приклад розширеного дерева
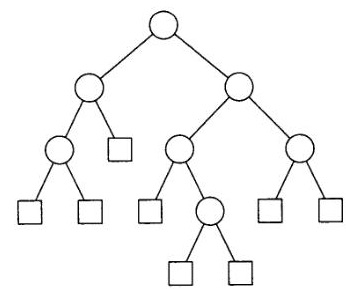

Припустимо, є наступний набір листя:
Тоді можна сформулювати наступні завдання:
- сконструювати бінарне дерево таким чином, щоб сума шляхів була мінімальною, так як це скорочує час обчислень для різних алгоритмів.
- сконструювати повне розширене бінарне дерево таким чином, щоб сума творів шляхів від кореневого вузла до листя на значення листового вузла була мінімальною.
Давид Хаффман (David Huffman) запропонував алгоритм для вирішення цієї проблеми, в якому на кожному кроці вибираються і складаються два найменших листа, як показано в лістингу 1, що призводить до дерева, зображеного на малюнку 4.
Лістинг 1. Приклад алгоритму Хаффмана
Малюнок 4. Бінарне дерево, побудоване за алгоритмом Хаффмана
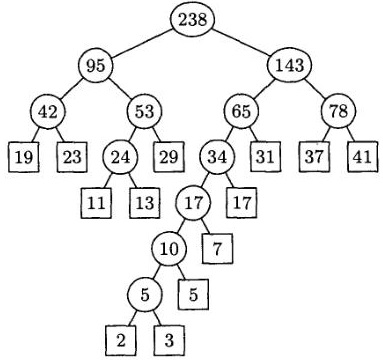

коди Хаффмана
Коди Хаффмана - це алгоритм, який використовується для стиснення даних. Нехай є якесь вихідне текстове повідомлення, що складається з 5 символів: a, b, c, d, e. і кожен символ має свою власну частоту:
Потрібно закодувати це повідомлення за допомогою 0 та 1 таким чином, щоб розмір результуючого рядка виявився мінімальним. У таблиці наведено приклад кодування символів для даного повідомлення:
Якщо зашифрувати повідомлення bcd за допомогою коду №1, то вийде - 001010011. За допомогою коду №2 можна робити те ж саме, але отримала рядок буде коротше - 1101001.
Тепер можна сформулювати саму проблему: необхідно підібрати такий алгоритм шифрування, при якому довжина зашифрованою рядки буде мінімальною.
У першому варіанті на кожен символ відводилося по 3 символу, а в другому варіанті - вже 2.2, але можна зробити ще коротше і отримати коефіцієнт, що дорівнює 2.15. Це робиться за допомогою алгоритму Хаффмана, в якому беруться 2 символи, які мають найменшу частоту, і об'єднуються, як два дочірніх вузла.
Алгоритм для рядка, що складається з 5 символів, реалізується в такий спосіб. На першому кроці об'єднуються два символу - a і d. як такі, що найменшу частоту. На другому в якості батька додається символ c. На третьому кроці додається символ e. і в кінці - символ b. В результаті виходить наступний код:
Висота бінарного дерева
Для визначення висоти дерева потрібно пройти від кореня спочатку по лівому Піддерево, потім по правому, порівняти ці дві висоти і вибрати максимальне значення. І не забути до одержали значенням додати одиницю (кореневої елемент). У лістингу 2 наведена рекурсивна функція для виконання цього завдання.
Лістинг 2. Визначення висоти дерева - рекурсивна реалізація на мові Сі
«Дзеркальне» відображення бінарного дерева
Коли два дерева є дзеркальним відображенням один одного, то йдеться, що вони симетричні. Для отримання «дзеркальної» копії дерева використовується алгоритм, наведений у лістингу 3. Спочатку виконується перевірка на наявність у кореня дерева дочірніх вузлів, і якщо ці вузли є, то вони міняються місцями. Потім ці ж дії рекурсивно повторюються для лівого і правого дочірніх вузлів. Якщо існує тільки один дочірній вузол, тоді можна переходити на один рівень нижче по дереву і продовжувати.
Лістинг 3. Реверс дерева - рекурсивна реалізація на мові Сі
Пошук вузла в бінарному дереві
Для пошуку вузла в бінарному дереві за що містяться в ньому значень можна використовувати функцію lookup. наведену в лістингу 4:
Лістинг 4. Пошук вузла в дереві - рекурсивна реалізація на мові Сі
Ширина бінарного дерева
Під шириною дерева розуміється максимальна кількість вузлів, які розташовані на одній висоті. Щоб визначити ширину дерева, досить просто додати лічильник в уже розглянутий алгоритм для визначення висоти дерева.
Лістинг 5. Визначення ширини дерева - рекурсивна реалізація на мові Сі
Кількість вузлів в бінарному дереві
Обчислити кількість вузлів в бінарному дереві також можна за допомогою рекурсії.
Лістинг 6. Обчислення кількості вузлів в дереві - рекурсивна реалізація на мові Сі
Порівняння бінарних дерев
Щоб визначити, чи збігаються два різних дерева, можна використовувати алгоритм з лістингу 7.
Лістинг 7. Порівняння бінарних дерев - рекурсивна реалізація на мові Сі
висновок
У даній статті була виконана класифікація бінарних дерев і розглянуті алгоритми для виконання найважливіших операцій: визначення висоти і ширини дерева, відображення дерева і пошук в ньому певного елемента. Також було розглянуто алгоритм Хаффмана, який може використовуватися для побудови розширених дерев і, як наслідок, для кодування інформації.
Ресурси для скачування
Схожі теми
- Робота зі структурами даних в мовах Сі та Python. Частина 1 .
- Робота зі структурами даних в мовах Сі та Python. Частина 2 .
- Робота зі структурами даних в мовах Сі та Python. Частина 3.
- Робота зі структурами даних в мовах Сі та Python. Частина 4.
- Робота зі структурами даних в мовах Сі та Python. Частина 5.
- Робота зі структурами даних в мовах Сі та Python. Частина 6.