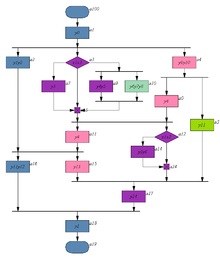
Приклад розбиття паралельної граф-схеми алгоритму логічного управління. У складі блоків, зазначених різними кольорами, немає паралельних вершин
Розбиття графа на підграфи (англ. Graph partition) (іноді в літературі також вживається термін розрізання графа [1]) - уявлення вихідного графа G = ⟨A. V⟩ у вигляді безлічі підмножин вершин S e p A = . A i ⊆ V
A = \ left \, A_. A_ \ right \>, A_ \ subseteq V> за певними правилами. Зазвичай за умовою задачі потрібно, щоб ⋃ i = 1 n A i = A ^ A_ = A>. тобто всі вершини вихідного графа повинні бути розподілені по підмножини, причому A i ≠ ∅ \ neq \ varnothing>. Зазвичай також додатково вводиться вимога ортогональності розбиття: ∀ i ≠ j A i ∩ A j = ∅
A_ \ cap A _ = \ varnothing>. тобто одна і та ж вершина не може входити до складу різних підмножин. Іноді з безлічі можливих розбиттів потрібно вибрати одне, яке задовольняє обмеженням і є оптимальним (або субоптимальних) за вказаною критерію, або довести, що шукане розбиття не існує (обмеження суперечливі). Завдання розбиття графа відноситься до класу NP-повних. верхня оцінка числа розбиття визначається числом Белла. однак при цьому зазвичай не всі можливі розбиття є коректними (не порушують обмежень), тобто оцінка є завищеною. При значеннях числа вершин графа N = | A | більше 15-20 отримання оптимальних розбиття як правило неможливо за прийнятний час (іноді для цього використовується метод гілок і меж), тому на практиці обмежуються субоптимальних рішеннями, отриманими з використанням евристичних алгоритмів.
Необхідність отримання розбиття виникає при вирішенні ряду завдань:
- Завдання розмальовки графа - кожне безліч вершин V i> складається з вершин одного кольору, причому вершини одного кольору не мають спільних інцидентних ребер. Зазвичай цікавить відшукання мінімальної розмальовки, що в загальному випадку є завданням класу NP (критерій оптимальності - n → min).
- Завдання визначення числа і складу компонент зв'язності графа.
- При проектуванні топології локальної мережі її розбиття на широкомовні домени визначається вимогами продуктивності (критерій оптимальності - обсяг переданого междоменной трафіку при використанні різних серверів і мережевих служб (доступ до файлових серверів. Службам DHCP. WINS. DNS і т. Д.), Обмеження - число портів і пропускна здатність комутаторів. маршрутизаторів і каналів зв'язку, а також вартість).
- У задачі трасування межсоединений друкованих плат або мікросхем необхідно розбиття вихідної схеми на шари (кожен з яких представляє собою планарний граф). Критерії оптимальності - мінімальне число шарів і межсоединений (фактично, собівартість виробництва), обмеження - габаритні розміри і вимоги термічної і електромагнітної сумісності електронних компонентів. [2]
- У задачі розбиття граф-схеми алгоритму на блоки з метою реалізації на багатопроцесорної системі або логічному мультіконтроллером. Критерії оптимальності - мінімальне число блоків, мінімальні ступеня дублювання сигналів мікрооперацій і логічних умов, мінімальне число міжмодульних передач управління, мінімальний трафік міжмодульних передач управління і даних; обмеження диктуються використовуваної елементної базою. [3] [4] [5] [6]
- Подання графа у вигляді ярусно-паралельної форми або граф-схеми алгоритму у вигляді безлічі перетинів (безлічі вершин у складі перетинів можуть бути неортогональної).
- Розбиття графа алгоритму на непересічні підграфи з подальшим їх розміщенням в процесорних елементах або елементах в складі ПЛІС при реалізації конвеєрної обробки даних (балансування навантаження). [7] [8]
Методи розбиття графа [9]
- покоординатно розбиття
- Рекурсивний інерційний метод поділу навпіл
- Розподіл мережі з використанням кривих Пеано
- Розподіл з урахуванням зв'язності (по суті, пошук в ширину)
- Алгоритм Керніган - Ліна (англ.)