Розгортка тора - це наближене рішення задачі щодо суміщення поверхні тора з площиною. Тому що поверхня тора відноситься до неразвертиваемим поверхонь. Якщо задані ортогональні проекції поверхні тора розгортка тора може бути виконана способом допоміжних циліндричних поверхонь. Відповідно до цього способу: поверхню тора α ділять на яке-небудь кількість рівних частин (в даному випадку 12 α1, α2. Α12) горизонтально- проектується площинами γ1, γ2. γ11, що проходять через центр тора. кожна з них піддається апроксимації (заміні) допоміжної циліндричною поверхнею β1, β2. β12, які будуються щодо поверхні тора.
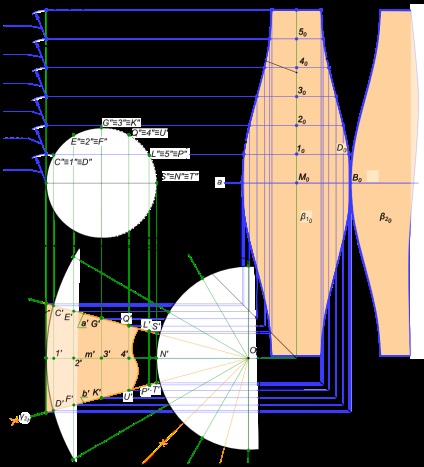
розгортка тора - виконується на прикладі (1/12) її частини, як розгорнення допоміжної циліндричної поверхні β1: - щоб розділити тор на рівні частини виконуємо розподіл нарисової окружності α` за допомогою циркуля, відзначаючи точки M`, M`1. M`11 і меридіани m`1, m`2. m`11, що проходять через них; - дві суміжних дуги нарисової окружності α` за допомогою циркуля ділимо навпіл і проводимо γ1H, γ2H; - ділимо дугу меридіана m "на дванадцять рівних частини відзначаючи точки M", 1 ", 2", 3 ", 4", 5 ", N"; - на горизонтальній проекції будуємо утворюють циліндричної поверхні β1 проходять через відмічені точки M`, 1 `, 2`, 3`, 4 `, 5`, N` і обмежені січними площинами в точках A` B`, C` D`, G `K`, Q`U`, L`P`, S`T` відповідно; - на фронтальній площині проекцій виконуємо розгортку меридіана m ". Підготовчі побудови закінчені, приступаємо до побудови розгортки циліндричної поверхні β1: - проводимо горизонтальну пряму a проходить через центр тора; - в прямокутній системі координат будуємо постійної пряму kO; - по лініях зв'язку будуємо точки розгортки і з'єднавши їх плавними лініями отримуємо фігуру A0 S0 T0 B0, яка представляє собою наближену розгортку половини поверхні тора α1; - добудувавши до неї другу половину симетрично щодо лінії a отримаємо розгортку β10 відповідного повної поверхні α1; - вся розгортка тора α може бути отримана прилаштовуванням до β10, однією за одною, 11 фігур конгруентність β10.