Визначення. Нехай випадкові величини ξ1. ξ2. ..., ξn - незалежні, і кожна з них має стандартний нормальний распределеніеN (0, 1). Кажуть, що випадкова величина χ 2n певна як
,
має розподіл хі-квадрат сn ступенями свободи.
Для Позначений ня цього розподілу також зазвичай використовується вираз χ 2n.
Ясно, що χ 2n (для будь-якого п≥ 1) з ймовірністю 1 набуває додатних значень. Функція щільності χ 2n в точці х (х> 0) дорівнює
.
де Г (-) - є гамма-функція. На практиці ця щільність розподілу безпосередньо використовується рідко.
Нижче зображені функції щільності розподілу хі-квадрат з різним числом ступенів свободи.
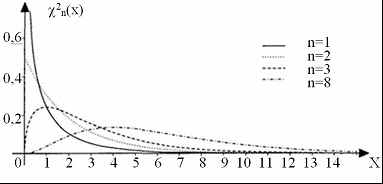
Мал. Функції щільності розподілу хі-квадрат з різним числом ступенів свободи п
Математичне сподівання і дисперсія випадкової величини χ 2n рівні:
,
.
Для випадкової величини χ 2n складені різноманітні таблиці. Найчастіше вони містять значення р- квантилів випадкових величин χ 2n. n = 1, 2. m (якщо ймовірність виражена у відсотках, їх називають процентними точками і, відповід ного, кажуть про таблиці процентних точок). Аргумент р, 0<р<1, при этом пробегает тот или иной набор значений.