Всі вироби можна розділити на неремонтіруемих і ремонтуються. Працездатність неремонтіруемих виробів після їх відмови не відновлюється. Це обумовлюється їх фізико-хімічними або конструктивними особливостями, а іноді економічними міркуваннями. Ці вироби можуть піддаватися профілактичного обслуговування.
Напрацювання від початку експлуатації неремонтіруемих вироби до його відмови називається напрацюванням до відмови або часом безвідмовної роботи. Напрацювання до відмови є безперервна випадкова величина. Відновлення роботи ремонтованого виробу після виникнення відмови передбачено конструктором при проектуванні цього виробу.
Часто вироби складаються з великої кількості елементів, кожен з яких відмовляє рідко. Імовірність появи одночасно двох відмов у таких виробах дорівнює нулю, і потік відмов називається ординарним. Якщо на ймовірність появи відмов на даному інтервалі часу не впливає наявність їх на будь-якому попередньому інтервалі, такий потік відмов називається потоком без наслідки.
У початковий період експлуатації складного вироби (період підробітки) середнє число відмов в одиницю часу постійно, і потік відмов називається нестаціонарним. Після закінчення періоду підробітки середнє число відмов в одиницю часу стає постійним.
- Розрахувати середню напрацювання до відмови Т розглянутих форсунок. Спочатку обчислення провести безпосередньо за вибірковими значеннями Т, а потім з використанням статистичного ряду.
Для обчислень середнього значення Т випадкової величини Т безпосередньо по її вибірковими значеннями t1. ti. tN використовують формулу:
Обчислення за допомогою статистичного ряду:
Весь діапазон спостережуваних значень Т розділити на m інтервалів або «розрядів» і підрахувати число значень ni. припадають на кожен i-ий розряд, і записати всі дані в таблицю.
Таблиця 1. Перетворення значень напрацювання до відмови в статистичний ряд.
Статистична ймовірність qi попадання випадкової величини на i- й інтервал розраховується як:
Відображаємо графічно отриманий статистичний ряд:
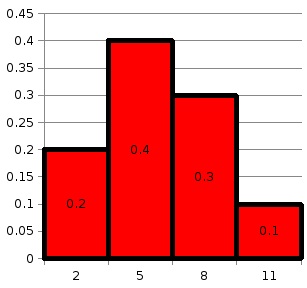
Мал. 1 Статистичний ряд значень напрацювання до відмови.
Для розрахунку середнього значення випадкової величини в якості «представника» всіх її значень, що належать i-му інтервалу, беруть його середину. Тоді середнє напрацювання до відмови визначається як (4)
Розрахунок з використанням формули (4) вносить деяку методичну помилку. Однак її значення зазвичай дуже малий. Цю помилку можна оцінити за формулою:
Де - середні значення.
Висновок: в даному завданні була розрахована середня напрацювання до відмови за вибірковими значеннями Т і з використанням статистичного ряду. Значення середнього наробітку по вибірці Т = 5,84 * 10 3 ч. Незначно відрізняється від значення з використанням статистичного ряду 5,96 * 10 3 ч.