Для заданого стержня необхідно:
- визначити положення центра ваги;
- обчислити головні центральні моменти інерції;
- побудувати епюру секториальной площі (полюс поміщаємо в центр ваги перерізу);
- обчислити секторіально-лінійний статичний момент;
- побудувати епюру головною секториальной площі (полюс поміщаємо в центр вигину);
- обчислити секторіальний момент інерції;
- обчислити момент інерції при чистому крученні;
- обчислити згинально-крутильне характеристику;
- записати диференціальне рівняння кутів закручування і граничні умови;
- обчислити внутрішні зусилля в стрижні і побудувати епюри (стрижень розбити на 4 ділянки);
- обчислити нормальні напруги в небезпечному перерізі і побудувати епюри.
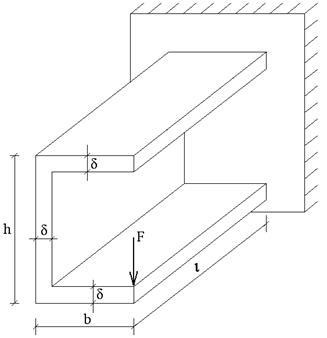
Схема перетину №1; точка прикладання сили 2;
1. Розбиваємо фігуру на найпростіші, визначаємо площі прямокутників.
2. Визначаємо положення центра ваги перерізу відносно осей
3. Обчислюємо головні центральні моменти інерції
4. Обчислюємо секторіальних площа.
Замінюємо швелер розрахункової схемою, яка відповідає осьовими лініями перетину. Будуємо епюри координат z і y.
Будуємо епюру секториальной площі (полюс вибираємо в центрі ваги перерізу P = C). 0 - початок відліку секториальной площі (на перетині контуру і осі симетрії).
де - координати точки початку елемента;
- координати точки кінця елемента.
Координати 1 (4,04; 9)
точок 2 (-9,46; 9)
відносно 3 (4,04; -9)
центру 4 (-9,46; -9)
тяжкості 0 (4,04; 0)
5. Визначаємо положення центра вигину.
Спочатку обчислюємо секторіально-лінійні статичні моменти, для цього множимо епюру на відповідні епюри координат (за способом Верещагіна).
(При множенні симетричною епюри на кососімметрічную результат дорівнює 0).
Визначаємо положення центра вигину.
6. Будуємо епюру головною секториальной площі (полюс поміщаємо в центр вигину P = D). 0 - початок відліку секториальной площі (на перетині контуру і осі симетрії).
Координати 1 (-5,5; 9)
відносно 3 (-5,5; -9)
0 - головна секториальная нульова точка - найближча до центру вигину нульова точка, у перетинів з однією віссю симетрії вона розташована на перетині контуру і цієї осі.
7. Обчислюємо секторіальний момент інерції.
Для цього перемножуємо епюру на епюру. (За способом Вере-
Щагін і формулою Сімпсона).
8. Обчислимо момент інерції при чистому крученні
9. Обчислимо згинально-крутильне характеристику
Попередньо обчислимо модуль зсуву:
10. Диференціальне рівняння кутів закручування
- інтенсивність зовнішньої розподіленої крутить навантаження з урахуванням знака (знак «плюс» коли навантаження прагне обертати проти годинникової стрілки при погляді з позитивного напрямку осі х)
Довільніпостійні залежать від граничних умов
Запишемо граничні умови
Для вільного торця ()
Для защемленного торця ()
11. Обчислимо внутрішні зусилля. Обчислення зведемо в таблицю.
Крутний момент при вільному крученні
Крутний момент при обмеженому крученні
У разі дії на стрижень зосередженої сили, у всіх перетинах має виконуватися умова: