Алгоритм обчислення найбільшого загального дільника (НСД) був відкритий давньогрецькими математиками і відомий як алгоритм "взаємного вирахування". І хоча згадка про це алгоритмі є ще у Аристотеля, згодом його стали називати алгоритмом Евкліда. Що таке найбільший спільний дільник, його властивості та методи обчислення розглянуті в [1].
Нагадаємо, що НСД двох чисел можна обчислити відповідно до наступної рекурентності:
На мові Сі процедура обчислення НОД має вид:
int gcd (int a, int b)
if (b == 0) return a;
return gcd (b, a% b);
Алгоритм Евкліда можна розширити для знаходження по заданих a і b таких цілих x та y. що ax + by = d. де d - найбільший спільний дільник a і b.
Тоді значення x і y. є рішеннями рівняння ax + by = d. знаходяться із співвідношень
x = y ', y = x' - y '· (2)
Через тут позначена ціла частина числа a / b.
Доведення. Оскільки a mod b = a - · b. то
d = x '· b + y' · (a - · b) = y '· a + (x' - y '·) · b = x · a + y · b,
де позначено x = y ', y = x' - y '·.
Функція gcdext (int a. Int b. Int * d. Int * x. Int * y), наведена нижче, за вхідними числах a і b знаходить d = НСД (a. B) і такі x. y що d = a · x + b · y. Для пошуку невідомих x і y необхідно рекурсивно запустити функцію gcdext (b. A mod b. D. X. Y) і перерахувати значення x і y по вище наведеною формулою. Рекурсія закінчується, коли b = 0. При b = 0 НСД (a. 0) = a і a = a · 1 + 0 · 0, тому вважаємо x = 1, y = 0.
void gcdext (int a, int b, int * d, int * x, int * y)
Для ручного виконання розширеного алгоритму Евкліда зручно скористатися таблицею з чотирма стовпцями (як показано нижче в прикладі), що відповідають значенням a. b. x. y. Процес обчислення розділимо на три етапи:
а) Спочатку обчислимо НСД (a. b), використовуючи перші два стовпці таблиці і співвідношення (1). В останньому рядку в колонці а буде знаходитися значення d = НСД (a. B).
б) Занесем значення 1 і 0 відповідно в колонки x та y останнього рядка.
в) Заповнюватимемо послідовно рядки для колонок x і y від низу до верху. Значення x і y в останній рядок вже занесені на етапі б). Вважаючи, що в поточній заповненої рядку вже знаходяться значення (x ', y'), ми за допомогою формул (2) будемо перераховувати і записувати значення (x. Y) у відповідні комірки вище стоїть рядки.
1. Розширений алгоритм Евкліда. Знайдемо рішення рівняння 5x + 3y = 1. Обчислення НСД (5, 3) і знаходження відповідних x. y зробимо в таблиці:
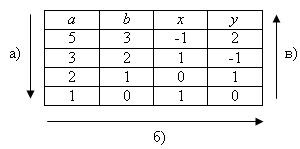
Порядок і напрямок обчислень вказані стрілками і буквами.
З таблиці знаходимо, що НОД (5, 3) = 5 · (-1) + 3 · 2 = 1, тобто x = -1, y = 2.
Розглянемо, наприклад, як отримані значення (x. Y) для першого рядка. З другого рядка беремо значення (x ', y') = (1, -1). За формулами (2) отримаємо:
y = x '- y' · = 1 - (-1) · = 1 + 1 = 2
Лінійним порівнянням називається рівняння виду ax = b (mod n). Воно має рішення тоді і тільки тоді, коли b ділиться на d = НСД (a. N). Якщо d> 1, то рівняння можна спростити, замінивши його на a 'x = b' (mod n '), де a' = a / d. b '= b / d. n '= n / d. Після такого перетворення числа a 'і n' є взаємно простими.
Алгоритм рішення рівняння a 'x = b' (mod n ') зі взаємно простими a' і n 'складається з двох частин:
1. Вирішуємо рівняння a 'x = 1 (mod n'). Для цього за допомогою розширеного алгоритму Евкліда шукаємо рішення (x0. Y0) рівняння a 'x + n' y = 1. Взявши за модулем n 'останню рівність, отримаємо a' x0 = 1 (mod n ').
Приклад. Вирішити рівняння 18x = 6 (mod 8).
Значення d = НСД (18, 8) = 2 є дільником 6, тому рішення існує. Після спрощення отримаємо рівняння 9x = 3 (mod 4). Що відповідно до леми еквівалентно 3x = 1 (mod 4). Вирішуючи рівняння 3x + 4y = 1 за допомогою розширеного алгоритму Евкліда, отримаємо x = -1, y = 1. Звідки x = -1 (mod 4) = 3. Тобто x = 3 буде як рішенням рівняння 3x = 1 (mod 4 ), так і 18x = 6 (mod 8).
Діофантових називаються рівняння виду
У цьому розділі розглянемо алгоритм знаходження рішення лінійного діофантових рівнянь з двома невідомими виду a · x + b · y = c (далі для простоти будемо опускати знаки множення і писати прото ax + by = c).
Теорема 1. Рівняння ax + by = c має рішення в цілих числах тоді і тільки тоді, коли c ділиться на НСД (a. B).
Теорема 2. Якщо пара (x0. Y0) є рішенням рівняння ax + by = c. то все безліч його рішень (x. y) описується формулою:
Для знаходження часткового вирішення (x0. Y0) рівняння ax + by = c слід спочатку знайти рішення (x ', y') рівняння ax + by = d (d - найбільший спільний дільник a і b) за допомогою розширеного алгоритму Евкліда, після чого помножити його на c / d. Тобто
Приклад. Знайти безліч рішень рівняння 5x + 3y = 7.
1. Рівняння має рішення, так як 7 ділиться на НСД (5, 3) = 1.
2. Знаходимо рішення рівняння 5x '+ 3y' = 1 за допомогою розширеного алгоритму Евкліда: (x ', y') = (-1, 2).
3. Знаходимо рішення (x0. Y0) вихідного діофантових рівнянь:
Згідно з теоремою 2 безліч рішень вихідного діофантових рівнянь має вигляд: