По відношенню до попередників новаторство Аполлонія виразилося, зокрема, в спільності, з якої він підійшов до свого предмету. Перш за все, Аполлоній визначив конічні перетину як перетину площиною, яка не зобов'язана бути перпендикулярної утворює конуса. Крім того, Аполлоній, як уже було сказано, розглядав і другу гілку гіперболи, а для цього врахував, що конус складається з двох порожнин. Це було необхідно для того, щоб теорії мали потрібну спільність - інакше довелося б домовлятися про занадто багато винятків. Таким чином, парабола перестала бути перетином тільки тупоугольного конуса, еліпс - остроугольного, а гіпербола - тупоугольного. Більш того: Аполлоній розглядав не тільки прямі кругові конуси (тобто такі, в яких перпендикуляр, опущений з вершини, проходить через центр підстави), а й довільні кругові конуси.
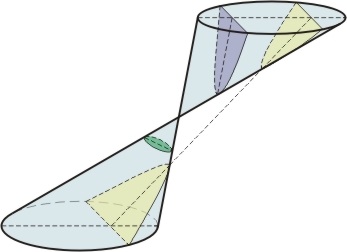
Мал. 1. Конічні перетини Аполону
Аполлоній показав, що перетину довільного конуса будь-якими площинами призводять тільки до цих трьох типів кривих (не рахуючи деяких вироджених випадків, наприклад, коли перетин складається з пари пересічних прямих). Саме тому він і повинен був змінити термінологію: замість «перетину прямокутного (остроугольного, тупоугольного) конуса» Аполлоній ввів терміни «парабола», «еліпс», «гіпербола». На минулому уроці ми бачили, що ці терміни пов'язані з формою рівнянь ( «симптомів»), що визначають дане перетин. Аполлоній показав, що співвідношення між координатами, яке виражається симптомом даного перетину:
y 2 = 2 px для параболи,
y 2 = 2 px - (p / a) x 2 для еліпса,
y 2 = 2 px + (p / a) x 2 для гіперболи,
не змінюється, якщо за вісь абсцис брати не тільки вісь конічного перетину.
Тут необхідно ввести новий термін. Діаметрами еліпса або гіперболи називаються будь-які відрізки, що проходять через центр еліпса або гіперболи. (Сподіваюся, ви розумієте, що таке центр гіперболи? Це її центр симетрії - точка перетину асимптот.) А діаметром параболи називається будь-яка пряма, паралельна осі параболи (тобто перетинає параболу рівно в одній точці). Так ось, Аполлоній показав, що симптом конічного перетину матиме той же самий вид, якщо вісь абсцис є довільним діаметром даного конічного перетину, а вісь ординат - дотичній в одному з кінців цього діаметра. Таким чином, це будуть вже не прямокутні координати: абсциси будуть відрізками діаметра, а ординати - полухордамі, паралельними відповідної дотичній. (У конічних перетинів є властивість, що хорди, паралельні цієї дотичної, діляться навпіл даними діаметром).
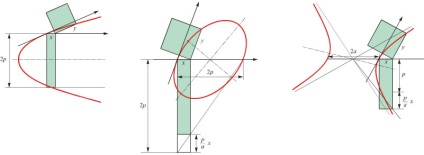
Мал. 2. Форма рівнянь конічних перетинів зберігається в координатах, утворених діаметром і дотичній
У разі еліпса і гіперболи для кожного діаметра можна визначити пов'язаний йому діаметр, тобто діаметр, паралельний дотичним, проведеним в кінцях вихідного діаметра.
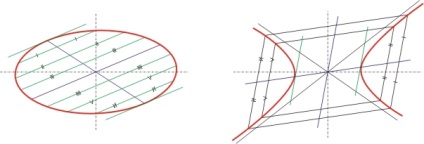
Мал. 3. Парні діаметри
Парні діаметри грають велику роль в теорії Аполлонія. Зокрема, він доводить, що:
- сума квадратів пов'язаних діаметрів еліпса постійна;
- паралелограм, побудований на сполучених діаметрах еліпса, має постійну площу.
Аполлоній багато займається питаннями про вигляді рівнянь конічних перетинів по відношенню до осей координат, що збігається з двома різними діаметрами, зокрема, сполученими. У сучасних позначеннях, рівняння еліпса і гіперболи по відношенню до зв'язаних діаметрів (так звані центральні рівняння еліпса і гіперболи) виглядають так:
x 2 / a 2 + y 2 / b 2 = 1 (еліпс),